Weil algebra of a Lie algebra

Let be a connected Lie group with Lie algebra . The Weil algebra of was first introduced in a series of seminars by H. Cartan [a1], in part based on some unpublished work of A. Weil. As a differential graded algebra, it is given by the tensor product

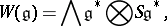where and denote the exterior and symmetric algebras, respectively (cf. also Exterior algebra; Symmetric algebra).

The Weil algebra and its generalizations have been studied extensively by F.W. Kamber and Ph. Tondeur [a3] [a4]. Let be a maximal compact subgroup, with denoting the Lie algebra of . The relative Weil algebra for is defined by

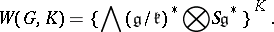With regards to the universal classifying bundle (cf. also Bundle; Classifying space; Universal space), there are canonical isomorphisms in cohomology

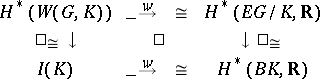where 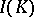denotes the 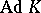-invariant polynomials. For a given integer , one has the ideal

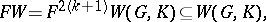generated by 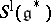, for 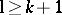. This leads to the truncated Weil algebra

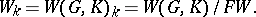The cohomology plays a prominent role in the study of secondary characteristic classes (cf. also Characteristic class) of foliations and foliated bundles [a3] (see also [a2]).

References

[a1]	H. Cartan, "Cohomologie réelle d'un espace fibré principal differentiable" , Sem. H. Cartan 1949/50, Exp. 19–20 (1950)
[a2]	J.L. Dupont, F.W. Kamber, "On a generalization of Cheeger–Chern–Simons classes" Illinois J. Math. , 34 (1990) MR1046564 Zbl 0724.57018
[a3]	F.W. Kamber, Ph. Tondeur, "Foliated bundles and characteristic classes" , Lecture Notes in Mathematics , 493 , Springer (1975) MR0402773 MR0385886 Zbl 0311.57011 Zbl 0308.57011
[a4]	F.W. Kamber, Ph. Tondeur, "Semi-simplicial Weil algebras and characteristic classes" Tôhoku Math. J. , 30 (1978) pp. 373–422 MR0509023 Zbl 0398.57006