Sard theorem
From Encyclopedia of Mathematics
Let 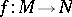 be a
be a 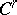 -mapping of manifolds
-mapping of manifolds 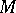 and
and 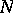 of dimensions
of dimensions  and
and  , respectively; if
, respectively; if  , then the critical values (cf. Critical value) of
, then the critical values (cf. Critical value) of 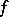 form a set of measure zero. The set of regular values turns out to be of full measure and everywhere dense. The theorem was proved by A. Sard [1].
form a set of measure zero. The set of regular values turns out to be of full measure and everywhere dense. The theorem was proved by A. Sard [1].
References
| [1] | A. Sard, "The measure of critical values of differentiable maps" Bull. Amer. Math. Soc. , 48 (1942) pp. 883–890 MR7523 Zbl 0063.06720 |
Comments
"Full measure" is, in the Russian article, called "massive setmassive" . See also Singularities of differentiable mappings.
How to Cite This Entry:
Sard theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sard_theorem&oldid=24559
Sard theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sard_theorem&oldid=24559
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article