Local tomography
Let 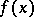 be a compactly supported piecewise-smooth function,
be a compactly supported piecewise-smooth function, 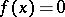 if
if 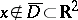 ,
, 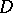 a bounded domain, and let
a bounded domain, and let 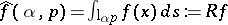 be its Radon transform, where
be its Radon transform, where 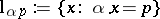 is the straight line parametrized by the unit vector
is the straight line parametrized by the unit vector 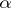 and a scalar
and a scalar 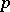 . The inversion formula which reconstructs
. The inversion formula which reconstructs 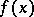 from the knowledge of
from the knowledge of 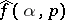 for all
for all  and all
and all 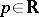 , where
, where 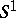 is the unit circle in
is the unit circle in 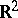 , is known to be:
, is known to be:
 | (a1) |
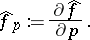 |
It is non-local: one requires the knowledge of  for all
for all 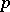 in order to calculate
in order to calculate 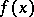 .
.
By local tomographic data one means the values of 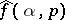 for those
for those 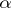 and
and 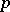 which satisfy the condition
which satisfy the condition 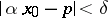 , where
, where 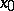 is a fixed "point of interest" and
is a fixed "point of interest" and 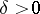 is a small number. Geometrically, local tomographic data are the values of the integrals over the straight lines which intersect the disc centred at
is a small number. Geometrically, local tomographic data are the values of the integrals over the straight lines which intersect the disc centred at 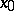 with radius
with radius 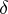 . In many applications only local tomographic data are available, while in medical imaging one wants to minimize the radiation dose of a patient and to use only the local tomographic data for diagnostics.
. In many applications only local tomographic data are available, while in medical imaging one wants to minimize the radiation dose of a patient and to use only the local tomographic data for diagnostics.
Therefore, the basic question is: What practically useful information can one get from local tomographic data?
As mentioned above, one cannot find 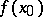 from local tomographic data.
from local tomographic data.
What does one mean by "practically useful information" ?
By this one means the location of discontinuity curves (surfaces, if 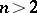 ) of
) of 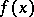 and the sizes of the jumps of
and the sizes of the jumps of 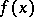 across these surfaces.
across these surfaces.
Probably the first empirically found method for finding discontinuities of 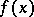 from local tomographic data was suggested in [a1], where the function
from local tomographic data was suggested in [a1], where the function
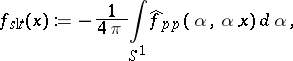 | (a2) |
which is the standard local tomography function, was proposed. To calculate 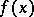 one needs to know only the local tomography data corresponding to the point
one needs to know only the local tomography data corresponding to the point  . It is proved that
. It is proved that 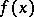 and
and 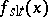 have the same discontinuities (but different sizes of the jumps across the discontinuity curves) [a11]. For various aspects of local tomography, see the references. See also Tomography.
have the same discontinuities (but different sizes of the jumps across the discontinuity curves) [a11]. For various aspects of local tomography, see the references. See also Tomography.
In [a7], [a8], [a9], a large family of local tomography functions was proposed. The basic idea here is to establish a relation between hypo-elliptic pseudo-differential operators and a class of linear operators acting on the functions 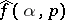 .
.
Let a pseudo-differential operator be defined by the formula 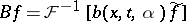 , where
, where 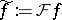 is the Fourier transform,
is the Fourier transform, 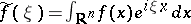 , and
, and  is a smooth function, which is called the symbol of
is a smooth function, which is called the symbol of 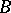 ,
, 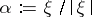 ,
, 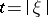 . If the symbol is hypo-elliptic, that is,
. If the symbol is hypo-elliptic, that is, 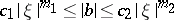 ,
, 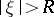 ,
, 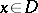 ,
, 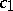 and
and 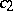 are positive constants, then
are positive constants, then 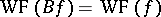 , where
, where 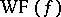 is the wave front of
is the wave front of 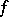 . Thus, the singularities of
. Thus, the singularities of 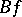 and
and 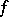 are the same. One can prove [a9] the formula
are the same. One can prove [a9] the formula 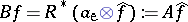 , where
, where 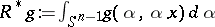 , where
, where 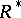 is the adjoint to the Radon operator
is the adjoint to the Radon operator 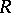 (cf. also Radon transform), and
(cf. also Radon transform), and 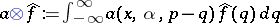 is the convolution operator, with distributional kernel
is the convolution operator, with distributional kernel  defined by
defined by
 |
and with
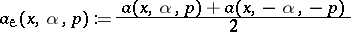 |
the even part of 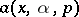 .
.
An operator 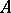 is called a local tomography operator if and only if
is called a local tomography operator if and only if  uniformly with respect to
uniformly with respect to 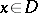 and
and 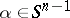 .
.
A necessary and sufficient condition for 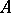 to be a local tomography operator is given in [a9]: The kernel
to be a local tomography operator is given in [a9]: The kernel 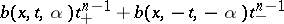 is an entire function of
is an entire function of 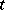 of exponential type
of exponential type 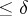 uniformly with respect to
uniformly with respect to 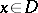 and
and 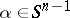 .
.
References
| [a1] | E. Vainberg, I. Kazak, V. Kurczaev, "Reconstruction of the internal  D structure of objects based on real-time integral projections" Soviet J. Nondestr. Test. , 17 (1981) pp. 415–423 (In Russian) D structure of objects based on real-time integral projections" Soviet J. Nondestr. Test. , 17 (1981) pp. 415–423 (In Russian) |
| [a2] | A. Faridani, E. Ritman, K. Smith, "Local tomography" SIAM J. Appl. Math. , 52 (1992) pp. 459–484 MR1174054 MR1154783 Zbl 0777.65076 Zbl 0758.65081 |
| [a3] | A. Katsevich, "Local tomography for the generalized Radon transform" SIAM J. Appl. Math. , 57 : 4 (1997) pp. 1128–1162 MR1462054 Zbl 0897.65084 |
| [a4] | A. Katsevich, "Local tomography for the limited-angle problem" J. Math. Anal. Appl. , 213 (1997) pp. 160–182 MR1469368 Zbl 0894.65065 |
| [a5] | A. Katsevich, "Local tomography with nonsmooth attenuation II" A.G. Ramm (ed.) , Inverse Problems, Tomography, and Image Processing , Plenum (1998) pp. 73–86 MR1625256 Zbl 0981.44002 |
| [a6] | A. Katsevich, "Local tomography with nonsmooth attenuation" Trans. Amer. Math. Soc. , 351 (1999) pp. 1947–1974 MR1466950 Zbl 0924.35207 |
| [a7] | A.G. Ramm, "Optimal local tomography formulas" PanAmer. Math. J. , 4 : 4 (1994) pp. 125–127 MR1310327 Zbl 0847.44001 |
| [a8] | A.G. Ramm, "Finding discontinuities from tomographic data" Proc. Amer. Math. Soc. , 123 : 8 (1995) pp. 2499–2505 MR1273517 Zbl 0830.44001 |
| [a9] | A.G. Ramm, "Necessary and sufficient conditions for a PDO to be a local tomography operator" C.R. Acad. Sci. Paris , 332 : 7 (1996) pp. 613–618 MR1386462 Zbl 0848.35147 |
| [a10] | A.G. Ramm, "New methods for finding discontinuities of functions from local tomographic data" J. Inverse Ill-Posed Probl. , 5 : 2 (1997) pp. 165–174 MR1452016 Zbl 0881.44003 |
| [a11] | A.G. Ramm, A.I. Katsevich, "The Radon transform and local tomography" , CRC (1996) MR1384070 Zbl 0863.44001 |
Local tomography. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Local_tomography&oldid=24499