Künneth formula
A formula expressing the homology (or cohomology) of a tensor product of complexes or a direct product of spaces in terms of the homology (or cohomology) of the factors.
Let 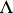 be an associative ring with a unit (cf. Associative rings and algebras), and let
be an associative ring with a unit (cf. Associative rings and algebras), and let 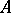 and
and 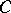 be chain complexes of right and left
be chain complexes of right and left 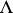 -modules, respectively. Let
-modules, respectively. Let  be the complex associated with the tensor product of
be the complex associated with the tensor product of 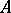 and
and 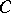 over
over 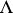 . If
. If
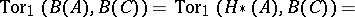 |
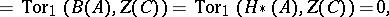 |
then there is an exact sequence of graded modules
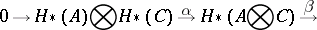 | (1) |
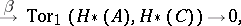 |
where 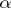 and
and 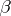 are homomorphisms of degree 0 and
are homomorphisms of degree 0 and 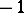 , respectively (see [2]). There is an analogous exact sequence for cochain complexes, with a homomorphism
, respectively (see [2]). There is an analogous exact sequence for cochain complexes, with a homomorphism 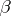 of degree 1. If
of degree 1. If 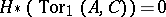 (e.g.
(e.g. 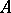 or
or 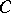 is a flat
is a flat 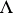 -module) and
-module) and 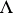 is hereditary, the sequence (1) exists and splits [2], [3], so that
is hereditary, the sequence (1) exists and splits [2], [3], so that
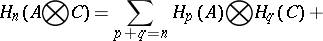 |
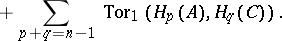 |
This is the Künneth formula; the term Künneth formula (or Künneth relation) is sometimes also applied to the exact sequence (1). There is a generalization of (1) in which the tensor product is replaced by an arbitrary two-place functor 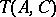 , on the category of
, on the category of 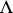 -modules with values in the same category, that is covariant in
-modules with values in the same category, that is covariant in 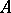 and contravariant in
and contravariant in 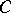 . In particular, the functor
. In particular, the functor 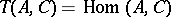 yields a formula expressing the cohomology
yields a formula expressing the cohomology 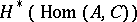 , where
, where 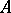 is a right chain complex and
is a right chain complex and  a left cochain complex over
a left cochain complex over 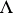 , in terms of
, in terms of 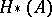 and
and 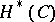 . Indeed, if
. Indeed, if 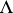 is hereditary and
is hereditary and 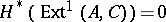 (e.g.
(e.g. 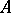 is free), one has the split exact sequence
is free), one has the split exact sequence
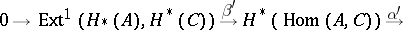 |
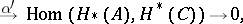 |
where 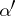 and
and 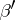 are homomorphisms of degree 0 and 1, respectively (see [2], [3]).
are homomorphisms of degree 0 and 1, respectively (see [2], [3]).
Let 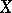 ,
, 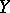 be topological spaces and let
be topological spaces and let 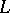 ,
, 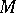 be modules over a principal ideal ring
be modules over a principal ideal ring 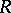 such that
such that 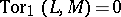 . Then the singular homologies of the spaces
. Then the singular homologies of the spaces 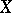 ,
, 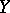 ,
, 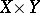 are connected by the following split exact sequence:
are connected by the following split exact sequence:
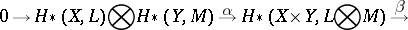 |
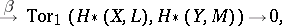 |
where 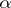 and
and 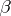 are homomorphisms of degree 0 and
are homomorphisms of degree 0 and 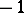 , respectively. If one assumes in addition that either all
, respectively. If one assumes in addition that either all 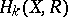 and
and 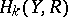 , or all
, or all 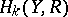 and
and 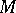 , are finitely generated, an analogous exact sequence is valid for the singular cohomologies:
, are finitely generated, an analogous exact sequence is valid for the singular cohomologies:
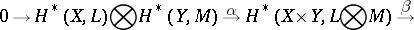 |
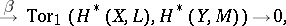 |
where 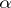 and
and 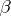 are homomorphisms of degree 0 and 1, respectively. For example, if
are homomorphisms of degree 0 and 1, respectively. For example, if 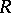 is a field, then
is a field, then
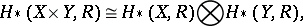 |
and if it is also true that all 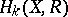 , or all
, or all 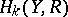 , are finite-dimensional, then
, are finite-dimensional, then
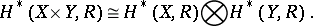 |
Similar formulas are available for the relative homology and cohomology [3], [4].
In the case 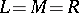 , the module
, the module 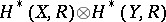 has the structure of a skew tensor product (cf. Skew product) of algebras, with
has the structure of a skew tensor product (cf. Skew product) of algebras, with 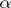 a homomorphism of algebras. Thus, if
a homomorphism of algebras. Thus, if 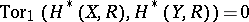 and all
and all 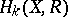 , or all
, or all 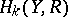 , are finitely generated, one has the following isomorphism of algebras [3]:
, are finitely generated, one has the following isomorphism of algebras [3]:
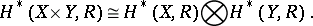 |
If 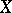 and
and 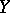 are finite polyhedra, the Künneth formula enables one to find the Betti numbers and torsion coefficients of the polyhedron
are finite polyhedra, the Künneth formula enables one to find the Betti numbers and torsion coefficients of the polyhedron 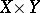 in terms of the analogous invariants of
in terms of the analogous invariants of 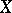 and
and 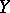 . These are in fact the original results of H. Künneth himself . In particular, if
. These are in fact the original results of H. Künneth himself . In particular, if 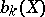 is the
is the 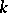 -th Betti number of the polyhedron
-th Betti number of the polyhedron 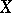 and if
and if
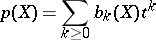 |
is its Poincaré polynomial, then 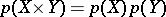 .
.
In the theory of cohomology with values in a sheaf there is yet another variant of the Künneth formula [6]. Let 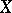 and
and 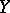 be topological spaces with countable bases, and let
be topological spaces with countable bases, and let 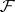 and
and 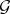 be Fréchet sheaves on
be Fréchet sheaves on 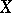 and
and 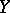 (see Coherent analytic sheaf). Suppose that
(see Coherent analytic sheaf). Suppose that 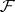 (or
(or 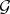 ) is a nuclear sheaf (i.e.
) is a nuclear sheaf (i.e. 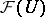 is a nuclear space for all open
is a nuclear space for all open 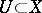 ). Then the Fréchet sheaf
). Then the Fréchet sheaf 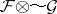 is defined on
is defined on 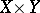 such that
such that
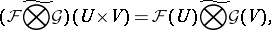 |
where 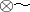 is the symbol for the completed tensor product and
is the symbol for the completed tensor product and 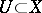 ,
, 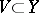 are open. If the spaces
are open. If the spaces 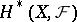 and
and 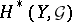 are separable, one has the Künneth formula
are separable, one has the Künneth formula
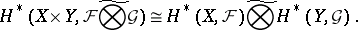 |
In particular, coherent analytic sheaves 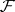 ,
, 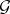 on complex-analytic spaces
on complex-analytic spaces 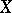 ,
, 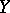 with countable bases are nuclear and
with countable bases are nuclear and
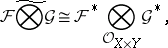 |
where 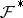 ,
, 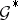 are the analytic inverse images of
are the analytic inverse images of 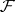 and
and 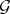 under the projections
under the projections 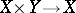 and
and 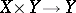 . Thus, if
. Thus, if 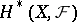 and
and 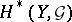 are separable, then
are separable, then
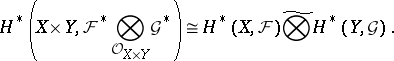 |
The Künneth formulas also figure in algebraic geometry, usually in the following version. Let 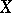 and
and 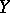 be algebraic varieties over a field
be algebraic varieties over a field 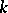 , and let
, and let 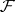 and
and 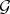 be coherent algebraic sheaves (cf. Coherent algebraic sheaf) on
be coherent algebraic sheaves (cf. Coherent algebraic sheaf) on 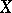 and
and 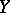 , respectively. Then [9]:
, respectively. Then [9]:
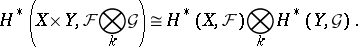 |
Here 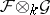 is the sheaf on
is the sheaf on 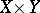 whose modules of sections over
whose modules of sections over 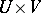 (
(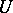 is an open affine subset of
is an open affine subset of 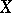 ,
, 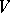 an open affine subset of
an open affine subset of 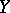 ) are
) are
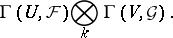 |
More generally, let 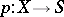 and
and 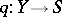 be morphisms (cf. Morphism) in the category of schemes, let
be morphisms (cf. Morphism) in the category of schemes, let 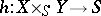 be their fibred product, and let
be their fibred product, and let 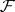 and
and 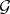 be quasi-coherent sheaves (cf. Quasi-coherent sheaf) of modules on
be quasi-coherent sheaves (cf. Quasi-coherent sheaf) of modules on 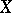 and
and 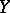 . Generalizing the construction of the sheaf
. Generalizing the construction of the sheaf 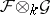 , one can introduce sheaves of modules
, one can introduce sheaves of modules 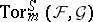 on
on 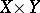 whose modules of sections for affine
whose modules of sections for affine 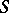 ,
, 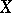 and
and 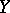 are isomorphic to
are isomorphic to 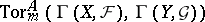 , where
, where 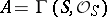 . Then [7] there exist two spectral sequences
. Then [7] there exist two spectral sequences 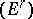 and
and 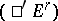 with initial terms
with initial terms
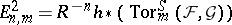 |
and
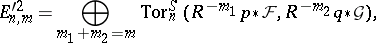 |
having the same limit. The awkward formulation of the Künneth formula assumes a more familiar form in terms of derived functors [11]:
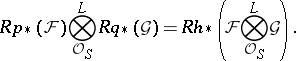 |
If the sheaves 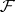 and
and 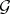 are flat over
are flat over 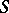 , then the spectral sequence
, then the spectral sequence 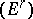 is degenerate. Similarly,
is degenerate. Similarly, 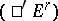 degenerates if all
degenerates if all 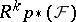 (or all
(or all 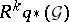 ) are flat over
) are flat over 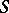 . If both spectral sequences
. If both spectral sequences 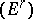 and
and 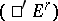 are degenerate, the Künneth formula becomes
are degenerate, the Künneth formula becomes
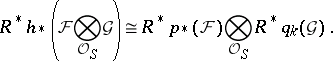 |
A Künneth formula is also valid for étale sheaves of 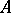 -modules on schemes
-modules on schemes 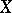 and
and 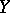 , where
, where 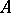 is a finite ring. It may be written as
is a finite ring. It may be written as
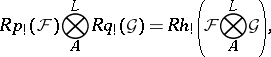 |
where the  means that the cohomology is taken with compact support. In particular (see [8]), if
means that the cohomology is taken with compact support. In particular (see [8]), if 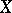 and
and 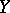 are complete algebraic varieties, the Künneth formula for the
are complete algebraic varieties, the Künneth formula for the 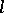 -adic cohomology is
-adic cohomology is
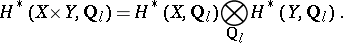 |
The formula has been proved for arbitrary varieties only on the assumption that the singularities can be resolved, e.g. for varieties over a field of characteristic zero.
There is also a version of the Künneth formula in 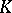 -theory. Let
-theory. Let 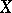 be a space such that the group
be a space such that the group 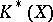 is finitely generated, and let
is finitely generated, and let 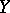 be a cellular space. Then there is an exact sequence of
be a cellular space. Then there is an exact sequence of 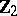 -graded modules
-graded modules
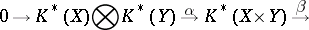 |
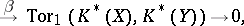 |
where 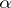 and
and 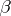 are homomorphisms of degree 0 and 1, respectively (see [5]). A particular case of this proposition is the Bott periodicity theorem for complex vector bundles. A Künneth formula is also known in bordism theory [10].
are homomorphisms of degree 0 and 1, respectively (see [5]). A particular case of this proposition is the Bott periodicity theorem for complex vector bundles. A Künneth formula is also known in bordism theory [10].
References
| [1a] | H. Künneth, "Ueber die Bettische Zahlen einer Produktmannigfaltigkeit" Math. Ann. , 90 (1923) pp. 65–85 |
| [1b] | H. Künneth, "Ueber die Torsionszahlen von Produktmannigfaltigkeiten" Math. Ann. , 91 (1924) pp. 125–134 |
| [2] | H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956) MR0077480 Zbl 0075.24305 |
| [3] | A. Dold, "Lectures on algebraic topology" , Springer (1980) MR0606196 Zbl 0434.55001 |
| [4] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) MR0210112 MR1325242 Zbl 0145.43303 |
| [5] | M.F. Atiyah, "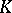 -theory: lectures" , Benjamin (1967) MR224083 -theory: lectures" , Benjamin (1967) MR224083 |
| [6] | L. Kaup, "Eine Künnethformel für Fréchetgarben" Math. Z. , 97 : 2 (1967) pp. 158–168 |
| [7] | A. Grothendieck, J. Dieudonné, "Eléments de géometrie algébrique" Publ. Math. IHES , 17 (1963) pp. Chapt. 3, Part 2 |
| [8] | M. Artin (ed.) A. Grothendieck (ed.) J.-L. Verdier (ed.) , Théorie des topos et cohomologie étale des schémas (SGA 4, vol. III) , Lect. notes in math. , 305 , Springer (1973) |
| [9] | J. Sampson, G. Washnitzer, "A Künneth formula for coherent algebraic sheaves" Illinois J. Math. , 3 : 3 (1959) pp. 389–402 |
| [10] | P.E. Conner, E.E. Floyd, "Differentiable periodic maps" , Springer (1964) MR0176478 Zbl 0125.40103 |
| [11] | R. Hartshorne, "Residues and duality" , Springer (1966) MR0222093 Zbl 0212.26101 |
Comments
More generally, cohomology theories have a Künneth formula spectral sequence for 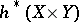 , where
, where 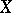 and
and 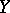 are as in the last section of the main article above (e.g., for equivariant
are as in the last section of the main article above (e.g., for equivariant 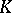 -theory see [a1]).
-theory see [a1]).
References
| [a1] | L. Hodgkin, "The equivariant Künneth theorem in 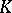 -theory" , Lect. notes in math. , 496 , Springer (1975) -theory" , Lect. notes in math. , 496 , Springer (1975) |
Künneth formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=K%C3%BCnneth_formula&oldid=24488