Function of exponential type
From Encyclopedia of Mathematics
An entire function  satisfying the condition
satisfying the condition
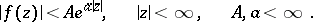 |
If  is represented by a series
is represented by a series
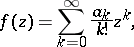 |
then
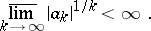 |
The simplest examples of functions of exponential type are  ,
,  ,
,  , and
, and  .
.
A function of exponential type has an integral representation
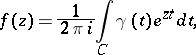 |
where 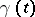 is the function associated with
is the function associated with 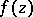 in the sense of Borel (see Borel transform) and
in the sense of Borel (see Borel transform) and 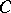 is a closed contour enclosing all the singularities of
is a closed contour enclosing all the singularities of  .
.
References
| [1] | B.Ya. Levin, "Distribution of zeros of entire functions" , Amer. Math. Soc. (1964) (Translated from Russian) MR0156975 Zbl 0152.06703 |
Comments
References
| [a1] | R.P. Boas, "Entire functions" , Acad. Press (1954) MR0068627 Zbl 0058.30201 |
How to Cite This Entry:
Function of exponential type. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Function_of_exponential_type&oldid=24449
Function of exponential type. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Function_of_exponential_type&oldid=24449
This article was adapted from an original article by A.F. Leont'ev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article