Fold

A type of singularity of differentiable mappings (cf. Singularities of differentiable mappings).

Let 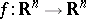be a 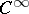-function. Then 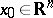is said to be a fold o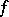f if

and if the Hessian of at 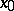is not equal to zero (cf. Hessian of a function). This definition can be generalized to the case of a 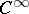-mapping 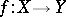between 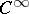-manifolds 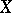and 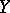(necessarily of the same dimension), cf. [a1].

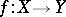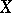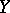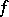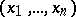The name derives from the following fact: If (with , and as above) has a fold at , then there are local coordinates in 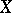vanishing at 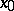and local coordinates in 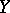vanishing at 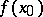such that 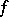has the local representation

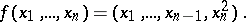References

[a1]	L.V. Hörmander, "The analysis of linear partial differential operators" , 3 , Springer (1985) MR1540773 MR0781537 MR0781536 Zbl 0612.35001 Zbl 0601.35001
[a2]	V.I. Arnol'd, S.M. [S.M. Khusein-Zade] Gusein-Zade, A.N. Varchenko, "Singularities of differentiable maps" , 1 , Birkhäuser (1985) (Translated from Russian) MR777682 Zbl 0554.58001