Control system

One of the central concepts in cybernetics. It is an object with a deterministic structure and possessing certain functional properties, reflecting their information processing character. The concept of a control system is related to a number of concepts which cannot be completely explained using only a mathematical language. Therefore, for a clarification of these concepts it is necessary to have an intuitive interpretation of them. Here are some (informal) examples of physical control system.

Nerve tissues consist of a structure of neurons and realize transformation of stimuli, coming from the outside and having effect on an organ.

A computer is an interconnection of elements and enables one to carry out a series of elementary commands.

Chemical molecules are characterized by a configuration of atoms and possess numerous properties of interest (properties of matter induced by a given structure of the molecules, e.g. of the colour and other physical features, etc.).

A chess position, assigning the figures on the board and the choice of an admissible move for one of the players.

A sentence in Russian, constructed from its alphabet according to the rules of grammar (syntax) and possessing a certain meaning (semantics).

Each of the objects mentioned exhibits a structure (or scheme) and specific properties or purposes. In considering these objects as control systems one is interested, grosso modo, in their behaviour-functional characteristics, without paying attention to the more detailed internal properties. Therefore, two control systems, having in some sense identical behaviour and identical purposes, are not regarded as distinct.

The mathematical development of the concepts of control systems consists in making precise the concepts of a behaviour and a purpose, as well as certain other details, taking into account the information flow and the interconnection of the parts of the control system. The first construction of a control system goes back to 1955 (cf. [1]). Later there appeared other more special types of control systems, the causal networks of A.A. Markov [2], the aggregates of N.P. Buslenko [3] and others. A complete definition of control systems was established in [1]. This definition includes all known definitions of a control system as particular cases. In view of the considerable complexity of giving a precise definition of a control system, below a brief description of four basic elements is given: schemes, information, coordinates, and functions.

A scheme of a control system is represented by a certain interconnection of elements, each of which is connected with a given memory, forming a so-called subscheme in it. The states of the memory, lying in a certain finite (or countable) set, specify the information in the memory of the control system. The interconnection of the scheme is characterized by a set of coordinates (also consisting of a finite or countable set) of elements. Finally, the function of a control system defines possible transformations of the control system, arising (deterministically or stochastically) at a moment in time, belonging to a certain discrete (at most countable) scale. These transformations can change the information in the memory (changing the state parameters), can realize motions of the control system (changing the coordinates of the elements), or can change the scheme (structure) and the function (behaviour).

Examples show that the scheme and function in a control system may have various meanings. Thanks to this fact control systems can serve as descriptions of physical systems in an adequate way, i.e. preserving their functional properties and their structure (schemes). Thus, control systems are powerful means for modelling system, and are sufficiently rich to copy not only the behaviour of the objects, but also their schemes.

Since every elementary subsystem of a given control system actually defines itself a certain elementary control system, it follows that the initial control system may be considered as a certain complex system, or as a union of elementary control systems. This is why one speaks not of defining the concept of a control system, but of a refinement, in which one control system is considered as being composed of other elementary ones, taken as undefined. It is necessary to mark off the width of the concept of a control system, which is suitable for describing not only simple discrete transformations, but also objects with complex functions and structures. This allows one to describe a computer, robots, adaptive systems with variable structure, "learning" systems, etc.

Control systems as mathematical models of initial physical control systems, studied in cybernetics, possess a number of characteristic features. First of all, they include objects of a discrete character. The discreteness is apparent in the scheme, its coordinates, its information, its function, and in the discreteness of the time. For control systems satisfying special cybernetic considerations, the character is more complicated. This complexity consists of the fact that the control system may have a large number of elements, a more complicated structure of the interconnections, a more complicated memory (as well as more complex information flow), and a more complicated behaviour. Real objects may be considered as control systems, generally speaking, in many ways. The synthesis of a control system depends on the choice of the elementary control systems and may be realized in different "hierarchies" . Thus, a control system has the property of relativity. The possibility of choosing the elementary control systems with different levels allows one in many cases to consider the initial control system as a hierarchy of control systems, in which the elementary control systems are on the highest level, and the relatively elementary control systems are on the next highest level. In this case one says that the control system has a hierarchical structure.

Finally, as a rule a control system does not describe the initial object completely, but only within certain error bounds. Owing to this fact one should regard it as an approximation to the object.

There have been attempts to extend the notion of a control system to continuous objects. As a result one has "continuous" control systems, and also "continuous-discrete" control systems. In addition, related objects have long been studied in the theory of dynamical systems and the theory of regulation. Among the discrete and continuous control systems there are internal resemblances, but more often there are great differences. The radical difference consists of the fact that a discrete control system describes an information processing system, while a continuous one describes an "energetic" process.

The study of control systems is carried out in special classes of control systems, according to the objects modelled. The type of object modelled is chosen according to the following considerations: a) their number should be small; b) they should be pairwise dissimilar; c) they should include a large number of common types; and d) they should give the possibility of forming from the given types a basis for constructing other types of control system. Below a list of types of modelling objects is given.

1) A formula of the algebra of logic in a given basis, realized by a Boolean function (in particular, disjunctive normal forms).

2) A diagram of functional elements in a given basis and the realization by a system of Boolean functions.

3) A contact scheme, realized by a matrix of Boolean functions.

4) An automaton in a certain automata basis, which realizes the transformation of "input" sequences into "outputs" (cf. Automaton, finite).

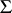5) An operator algorithm, realizing a computable function. For a given object to be modelled it is characteristic that every control system is completely defined by its scheme and function , i.e. by the pair . Here 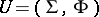. On the other hand, for every class 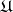of objects to be modelled there exists a function such that 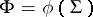, i.e. the function is uniquely defined by the scheme. Moreover, is a computable function. In this case every element of the class to be modelled can be characterized in another way. Let and 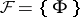, where 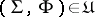. The class 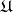is completely defined by the given sets 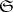and 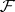, and thus by the specification of an algorithm 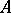to compute .

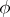The basic problem in the theory of control systems circle around three questions (cf. [4]): The problem of synthesis (cf. Synthesis problems), the problem of equivalent transformations of control systems, and the problem of their reliability (cf. Reliability and inspection of control systems). A comparison of the results obtained for these problems for different classes of objects to be modelled shows that one has complete conformity in the formulation of corresponding theorems, and an observed similarity of proofs of the theorems mentioned; the proofs of theorems for more complex control systems often correspond closely to that of the corresponding theorems for simpler classes.

References

[1]	S.V. Yablonskii, "The basic concepts of cybernetics" Problems of cybernetics , 2 (1961) pp. 317–355 Problemy Kibernetiki , 2 (1959) pp. 7–38 Zbl 0123.12412
[2]	A.A. Markov, "Cybernetics, thinking, living" , Moscow (1964) (In Russian)
[3]	N.P. Buslenko, Izv. Ak. Nauk SSSR. Ser. Tekhn. Kibernetika , 5 (1963) pp. 7–18
[4]	A.A. Lyapunov, S.V. Yalonskii, Problemy Kibernetiki , 9 (1963) pp. 5–22 Zbl 0524.01014 Zbl 0086.11701

Comments

A reference giving mathematical definitions of a, continuous or discrete, control system is [a1].

References

[a1]	R.E. Kalman, P.L. Falb, M.A. Arbib, "Topics in mathematical system theory" , McGraw-Hill (1969) MR0255260 Zbl 0231.49001