Hermite problem
The problem about the homogeneous arithmetical minima of positive  -ary quadratic forms with real coefficients. It is equivalent to the problem of the densest lattice packing of
-ary quadratic forms with real coefficients. It is equivalent to the problem of the densest lattice packing of  -dimensional balls of equal radius (see Geometry of numbers).
-dimensional balls of equal radius (see Geometry of numbers).
Let 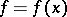 ,
,  , be a positive quadratic form over
, be a positive quadratic form over  of determinant
of determinant 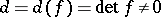 ; and let
; and let
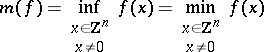 |
be its homogeneous arithmetical minimum. The quantity
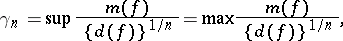 |
where the supermum or maximum is over all positive quadratic forms 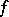 , is called the Hermite constant;
, is called the Hermite constant; 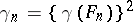 , where
, where 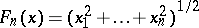 is the radial function corresponding to a ball.
is the radial function corresponding to a ball.
Originally, one understood by the Hermite problem the task of finding or estimating 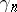 (from above and below). The exact values of
(from above and below). The exact values of 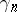 are known only for
are known only for  (see [1]). For estimates of
(see [1]). For estimates of 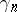 , see [2] or [1].
, see [2] or [1].
Subsequently, the term Hermite problem was used for the search for local maxima (boundary or extremal) of 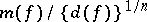 in the space of coefficients and their corresponding forms
in the space of coefficients and their corresponding forms 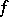 . Algorithms are known for finding all classes of boundary forms. In particular, the Voronoi algorithm for perfect forms (see [1], [3], [4]).
. Algorithms are known for finding all classes of boundary forms. In particular, the Voronoi algorithm for perfect forms (see [1], [3], [4]).
The problem was posed by Ch. Hermite in 1850.
References
| [1] | P.M. Gruber, C.G. Lekkerkerker, "Geometry of numbers" , North-Holland (1987) (Updated reprint) MR0893813 Zbl 0611.10017 |
| [2] | C.A. Rogers, "Packing and covering" , Cambridge Univ. Press (1964) MR0172183 Zbl 0176.51401 |
| [3] | B.N. Delone, "The Peterburg school of number theory" , Moscow-Leningrad (1947) (In Russian) |
| [4] | E.P. Baranovskii, "Packings, coverings, partitionings and certain other distributions in spaces of constant curvature" Progress in Math. , 9 (1971) pp. 209–253 Itogi Nauk. Mat. Algebra Topol. Geom. 1967 (1969) pp. 189–225 |
Hermite problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hermite_problem&oldid=24079