Genus of an element of an arithmetic group
The set of elements of the group 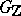 of units of a connected algebraic
of units of a connected algebraic 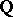 -group
-group 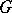 that are conjugate to a given element
that are conjugate to a given element  in the groups
in the groups 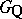 and
and 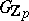 for all primes
for all primes 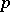 , where
, where 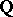 and
and  are the field of rational numbers and the ring of
are the field of rational numbers and the ring of  -adic integers, respectively. The class of the element
-adic integers, respectively. The class of the element  is defined as its conjugacy class in
is defined as its conjugacy class in 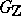 . The number of disjoint classes into which the genus of an element
. The number of disjoint classes into which the genus of an element  decomposes is finite [1], is denoted by
decomposes is finite [1], is denoted by 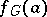 , and is called the number of classes in the genus of the element
, and is called the number of classes in the genus of the element  . The function
. The function 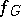 on
on  arising here is an important arithmetic characteristic expressing the deviation from the local-global principle in questions of conjugacy. In general,
arising here is an important arithmetic characteristic expressing the deviation from the local-global principle in questions of conjugacy. In general, 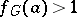 . Moreover, if the group
. Moreover, if the group  is semi-simple and the group
is semi-simple and the group 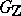 is infinite, then
is infinite, then 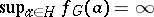 for any arithmetic subgroup
for any arithmetic subgroup 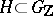 (see [1], [3]). The notions considered are a natural modification of the corresponding classical concepts in the theory of quadratic forms and are used in studies of residual approximability of arithmetic groups relative to conjugacy (see [2]).
(see [1], [3]). The notions considered are a natural modification of the corresponding classical concepts in the theory of quadratic forms and are used in studies of residual approximability of arithmetic groups relative to conjugacy (see [2]).
References
| [1] | V.P. Platonov, "On the genus problem in arithmetic subgroups" Soviet Math. Dokl. , 12 : 5 (1971) pp. 1503–1507 Dokl. Akad. Nauk SSSR , 200 : 4 (1971) pp. 793–796 |
| [2] | V.P. Platonov, G.V. Matveev, "Abelian groups and the finite approximability of linear groups with respect to conjugacy" Dokl. Akad. Nauk Bel.SSR , 14 : 9 (1970) pp. 777–779 (In Russian) MR0274603 |
| [3] | A.S. Rapinchuk, "Platonov's conjecture on the genus in arithmetic groups" Dokl. Akad. Nauk Bel.SSR , 25 : 2 (1981) pp. 101–104; 187 (In Russian) (English summary) MR613414 |
Genus of an element of an arithmetic group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Genus_of_an_element_of_an_arithmetic_group&oldid=24076