Homology of a complex
The starting point for various homological constructions. Let  be an Abelian category and let
be an Abelian category and let  be a chain complex in
be a chain complex in 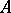 , i.e. a family of objects
, i.e. a family of objects 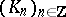 in
in 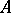 and morphisms
and morphisms 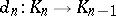 such that
such that  for all
for all  . The quotient object
. The quotient object  is called the
is called the  -th homology of the complex
-th homology of the complex  and is denoted by
and is denoted by  . The family
. The family  is also denoted by
is also denoted by  . The concept of the homology of a complex serves as the base for a number of important constructions in homological algebra, commutative algebra, algebraic geometry, and topology. Thus, in topology, each topological space
. The concept of the homology of a complex serves as the base for a number of important constructions in homological algebra, commutative algebra, algebraic geometry, and topology. Thus, in topology, each topological space  defines a chain complex in the category
defines a chain complex in the category  of Abelian groups:
of Abelian groups:  . Here
. Here  is the group of
is the group of  -dimensional singular chains of
-dimensional singular chains of  , while
, while  is the boundary homomorphism. The
is the boundary homomorphism. The  -th homology of this complex is said to be the
-th homology of this complex is said to be the  -th singular homology group of
-th singular homology group of  and is denoted by
and is denoted by  . The concept of the cohomology of a cochain complex is defined in a dual manner.
. The concept of the cohomology of a cochain complex is defined in a dual manner.
References
| [1] | S. MacLane, "Homology" , Springer (1963) Zbl 0818.18001 Zbl 0328.18009 |
Comments
References
| [a1] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) MR0210112 MR1325242 Zbl 0145.43303 |
Homology of a complex. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Homology_of_a_complex&oldid=23860