Hodge structure
of weight  (pure)
(pure)
An object consisting of a lattice 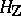 in the real vector space
in the real vector space 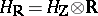 and a decomposition
and a decomposition 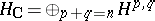 of the complex vector space
of the complex vector space 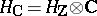 (a Hodge decomposition). Here the condition
(a Hodge decomposition). Here the condition 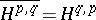 must hold, where the bar denotes complex conjugation in
must hold, where the bar denotes complex conjugation in 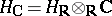 . Another description of the Hodge decomposition consists in the specification of a decreasing filtration (a Hodge filtration)
. Another description of the Hodge decomposition consists in the specification of a decreasing filtration (a Hodge filtration) 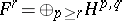 in
in 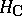 such that
such that 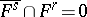 for
for  . Then the subspace
. Then the subspace 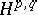 can be recovered by the formula
can be recovered by the formula 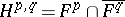 .
.
An example is the Hodge structure in the  -dimensional cohomology space
-dimensional cohomology space 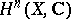 of a compact Kähler manifold
of a compact Kähler manifold 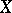 , which was first studied by W.V.D. Hodge (see [1]). In this case the subspace
, which was first studied by W.V.D. Hodge (see [1]). In this case the subspace 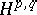 can be described as the space of harmonic forms of type
can be described as the space of harmonic forms of type 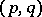 (cf. Harmonic form), or as the cohomology space
(cf. Harmonic form), or as the cohomology space 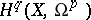 of sheaves
of sheaves 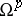 of holomorphic differential forms [2]. The Hodge filtration in
of holomorphic differential forms [2]. The Hodge filtration in 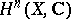 arises from the filtration of the sheaf complex
arises from the filtration of the sheaf complex 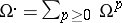 , the
, the  -dimensional hypercohomology group of which is
-dimensional hypercohomology group of which is 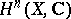 , by subcomplexes
, by subcomplexes 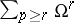 .
.
A more general concept is that of a mixed Hodge structure. This is an object consisting of a lattice 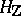 in
in 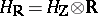 , an increasing filtration (a filtration of weights)
, an increasing filtration (a filtration of weights) 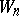 in
in 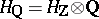 and a decreasing filtration (a Hodge filtration)
and a decreasing filtration (a Hodge filtration) 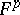 in
in 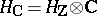 , such that on the space
, such that on the space  , the filtrations
, the filtrations 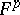 and
and  determine a pure Hodge structure of weight
determine a pure Hodge structure of weight  . The mixed Hodge structure in the cohomology spaces of a complex algebraic variety (not necessarily compact or smooth) is an analogue of the structure of the Galois module in the étale cohomology (cf. [3]). The Hodge structure has important applications in algebraic geometry (see Period mapping) and in the theory of singularities of smooth mappings (see [4]).
. The mixed Hodge structure in the cohomology spaces of a complex algebraic variety (not necessarily compact or smooth) is an analogue of the structure of the Galois module in the étale cohomology (cf. [3]). The Hodge structure has important applications in algebraic geometry (see Period mapping) and in the theory of singularities of smooth mappings (see [4]).
References
| [1] | W.V.D. Hodge, "The theory and application of harmonic integrals" , Cambridge Univ. Press (1952) MR0051571 |
| [2] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , 1 , Wiley (Interscience) (1978) MR0507725 Zbl 0408.14001 |
| [3] | P. Deligne, "Poids dans la cohomologie des variétés algébriques" R. James (ed.) , Proc. Internat. Congress Mathematicians (Vancouver, 1974) , 1 , Canad. Math. Congress (1975) pp. 79–85 MR0432648 Zbl 0334.14011 |
| [4] | A.N. Varchenko, "Asymptotic integrals and Hodge structures" J. Soviet Math. , 27 (1984) pp. 2760–2784 Itogi Nauk. i Tekhn. Sovrem. Probl. Mat. , 22 (1983) pp. 130–166 Zbl 0554.58002 |
See also the references to Period mapping.
Comments
A Hodge structure of weight  thus consists of i) a finitely-generated Abelian group
thus consists of i) a finitely-generated Abelian group 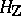 ; and ii) a finite decreasing filtration
; and ii) a finite decreasing filtration 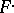 on
on  such that
such that  as soon as
as soon as 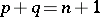 . A polarization of a Hodge structure of weight
. A polarization of a Hodge structure of weight  is a
is a 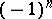 -symmetric
-symmetric 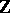 -valued bilinear form
-valued bilinear form 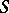 on
on 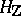 such that
such that 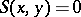 for
for 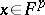 ,
, 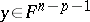 and such that
and such that 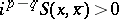 for
for  . The Hodge structures arising in algebraic geometry are always polarizable.
. The Hodge structures arising in algebraic geometry are always polarizable.
There exist classifying spaces for polarized Hodge structures with given numerical data [a1], as well as for mixed Hodge structures with a polarization on graded quotients for the weight filtration [a2]. Mixed Hodge structures form an Abelian category in which every morphism is strictly compatible with both Hodge and weight filtrations. Pure polarized Hodge structures form a Tannakian category [a3]. There exist canonical and functorial mixed Hodge structures on (local) cohomology groups of algebraic varieties , rational homotopy groups [a5], vanishing cycle groups of function germs [a6], [a7], and on the intersection homology groups of algebraic varieties with coefficients in a polarizable variation of Hodge structure [a8], [a9]. In the latter case, there is even a pure Hodge structure. At this moment (1989), the ultimate generalization seems to be the concept of a mixed Hodge module [a10]–[a11].
References
| [a1] | P. Griffiths, "Periods of integrals on algebraic manifolds" Amer. J. Math. , 90 (1968) pp. 568–625; 805–865 MR0242844 MR0233825 MR0229641 Zbl 0188.24801 Zbl 0183.25501 Zbl 0169.52303 |
| [a2] | J. Carlson, E. Cattani, A. Kaplan, "Mixed Hodge structures and compactifications of Siegel's space" A. Beauville (ed.) , Algebraic geometry (Angers, 1979) , Sijthoff & Noordhoff (1980) pp. 77–105 MR605337 |
| [a3] | N. Saavedra Rivano, "Catégories Tannakiennes" , Lect. notes in math. , 265 , Springer (1972) Zbl 0246.14003 Zbl 0241.14008 |
| [a4a] | P. Deligne, "Théorie de Hodge II, III" Publ. Math. IHES , 40 (1971) pp. 5–58 MR498551 |
| [a4b] | P. Deligne, "Théorie de Hodge IV" Publ. Math. IHES , 44 (1975) pp. 5–77 |
| [a5] | R.M. Hain, "The de Rham homotopy theory of complex algebraic varieties I, II"  -theory , 1 (1987) pp. 271–324; 481–497 -theory , 1 (1987) pp. 271–324; 481–497 |
| [a6] | J.H.M. Steenbrink, "Mixed Hodge structure on the vanishing cohomology" P. Holm (ed.) , Real and Complex Singularities (Oslo, 1976). Proc. Nordic Summer School , Sijthoff & Noordhoff (1977) pp. 525–563 MR0485870 Zbl 0373.14007 |
| [a7] | V. Navarro Aznar, "Sur la théorie de Hodge–Deligne" Invent. Math. , 90 (1987) pp. 11–76 Zbl 0639.14002 |
| [a8] | E. Cattani, A. Kaplan, W. Schmid, "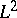 and intersection cohomologies for a polarizable variation of Hodge structure" Invent. Math. , 87 (1987) pp. 217–252 MR870728 Zbl 0611.14006 and intersection cohomologies for a polarizable variation of Hodge structure" Invent. Math. , 87 (1987) pp. 217–252 MR870728 Zbl 0611.14006 |
| [a9] | M. Kashiwara, T. Kawai, "The Poincaré lemma for variations of Hodge structure" Publ. RIMS Kyoto Univ. , 23 : 2 (1987) pp. 345–407 Zbl 0629.14005 |
| [a10] | M. Saito, "Modules de Hodge polarisables" Preprint RIMS , 553 (Oct. 1986) MR1000123 Zbl 0691.14007 |
| [a11] | M. Saito, "Mixed Hodge modules" Preprint RIMS , 585 (July 1987) MR2843222 MR1308540 MR1159259 MR1047741 MR1047415 MR1054250 MR1042805 MR0888149 MR0888148 Zbl 05986955 Zbl 0826.32029 Zbl 0815.14008 Zbl 0727.14004 Zbl 0726.14007 Zbl 0753.32004 Zbl 0765.14006 Zbl 0635.14009 Zbl 0635.14008 |
Hodge structure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hodge_structure&oldid=23854