Poincaré-Hopf theorem

Let 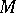be a smooth compact manifold with boundary , and let 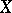be a vector field on 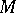with isolated zeros such that 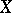points outwards at all points in the boundary .

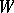Then the sum of the indices of the zeros of (see Singular point, index of a) is equal to the Euler characteristic of .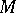

This is the generalization proved by H. Hopf, in 1926, of the two-dimensional version owed to H. Poincaré (1881, 1885) (see Poincaré theorem).

References

[a1]	J.W. Milnor, "Topology from the differentiable viewpoint" , Univ. Virginia Press (1965) pp. 35
[a2]	N.G. Lloyd, "Degree theory" , Cambridge Univ. Press (1978) pp. 33