Liénard equation
A non-linear second-order ordinary differential equation
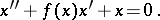 | (*) |
This equation describes the dynamics of a system with one degree of freedom in the presence of a linear restoring force and non-linear damping. If the function  has the property
has the property
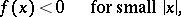 |
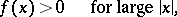 |
that is, if for small amplitudes the system absorbs energy and for large amplitudes dissipation occurs, then in the system one can expect self-exciting oscillations (the appearance of auto-oscillations, cf. Auto-oscillation). Sufficient conditions for the appearance of auto-oscillations in the system (*) were first proved by A. Liénard [1].
The Liénard equation is closely connected with the Rayleigh equation. An important special case of it is the van der Pol equation. Instead of equation (*) it is often convenient to consider the system
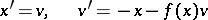 |
(a stable limit cycle on the phase plane  is adequate for an auto-oscillating process in the system (*)), or the equivalent equation
is adequate for an auto-oscillating process in the system (*)), or the equivalent equation
 |
If one introduces a new variable  , where
, where  , then (*) goes into the system
, then (*) goes into the system
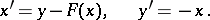 |
More general than the Liénard equation are the equations
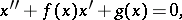 |
 |
The main interest is in the determination of possibly more general sufficient conditions under which these equations have a unique stable periodic solution. The non-homogeneous Liénard equation
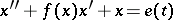 |
and generalizations of it have also been studied in detail.
References
| [1] | A. Liénard, Rev. Gen. Electr. , 23 (1928) pp. 901–912; 946–954 |
| [2] | A.A. Andronov, A.A. Vitt, A.E. Khaikin, "Theory of oscillators" , Dover, reprint (1987) (Translated from Russian) |
| [3] | G. Sansone, "Ordinary differential equations" , 2 , Zanichelli (1948) (In Italian) |
| [4] | S. Lefschetz, "Differential equations: geometric theory" , Interscience (1957) |
| [5] | R. Reissig, G. Sansone, R. Conti, "Nichtlineare Differentialgleichungen höherer Ordnung" , Cremonese (1969) |
Liénard equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Li%C3%A9nard_equation&oldid=23384