Lévy-Cramér theorem

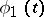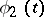If the sum of two independent non-constant random variables is normally distributed, then each of the summands is normally distributed. This result was stated by P. Lévy [1] and proved by H. Cramér [2]. Equivalent formulations are: 1) if the convolution of two proper distributions is a normal distribution, then each of them is a normal distribution; and 2) if and are characteristic functions and if

(*)

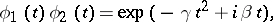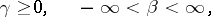then

In formulation 1), the Lévy–Cramér theorem admits a generalization to the convolution of two signed measures with restrictions on their negative variation; in formulation 2) it admits a generalization to the case when instead of condition (*) one considers the condition

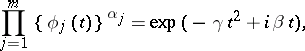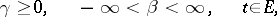where 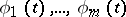are characteristic functions, 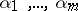are positive numbers and 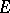is a set of real numbers with a limit point at the origin. There are generalizations of the Lévy–Cramér theorem to random variables in Euclidean spaces and in locally compact Abelian groups.

The Lévy–Cramér theorem has the following stability property. Closeness of the distribution of a sum of independent random variables to the normal distribution implies closeness of the distribution of each of the summands to the normal distribution; qualitative estimates of the stability are known.

Theorems analogous to the Lévy–Cramér theorem have been obtained for the Poisson distribution (Raikov's theorem), for the convolution of a Poisson and a normal distribution, and for other classes of infinitely-divisible distributions (see [6]).

References

[1]	P. Lévy, "Propriétés asymptotiques des sommes de variables aléatoires indépendantes ou enchaînées" J. Math. Pures Appl. , 14 (1935) pp. 347–402
[2]	H. Cramér, "Ueber eine Eigenschaft der normalen Verteilungsfunktion" Math. Z. , 41 (1936) pp. 405–414
[3]	D.A. Raikov, "On the decomposition of a Poisson law" Dokl. Akad. Nauk SSSR , 14 (1937) pp. 9–12 (In Russian)
[4]	Yu.V. Linnik, "On the decomposition of the convolution of Gaussian and Poissonian laws" Theory Probab. Appl. , 2 (1957) pp. 31–57 Teor. Veroyatnost. i Primenen. , 2 (1957) pp. 34–59
[5]	N.A. Sapogov, "On independent terms of a sum of random variables which is distributed almost normally" Vestn. Leningr. Univ. Ser. Mat. Mekh. Astr. , 14 : 19 (1959) pp. 78–105 (In Russian) (English abstract)
[6]	Yu.V. Linnik, I.V. Ostrovskii, "Decomposition of random variables and vectors" , Amer. Math. Soc. (1977) (Translated from Russian)
[7]	G.M. Fel'dman, "On the decomposition of Gaussian distributions on groups" Theory Probab. Appl. , 22 (1977) pp. 133–140 Teor. Veroyatnost. i Primenen. , 22 (1977) pp. 136–143

References

[a1]	Yu.V. Linnik, "Decomposition of probability laws" , Oliver & Boyd (1964) (Translated from Russian)
[a2]	E. Lukacs, "Characteristic functions" , Griffin (1960)
[a3]	E. Lukacs, R.G. Laha, "Applications of characteristic functions" , Griffin (1964)
[a4]	H.-J. Rossberg, B. Jesiah, G. Siegel, "Analytic methods of probability theory" , Akademie Verlag (1985)