Carathéodory theorem

on conformal mapping of domains with variable boundaries

One of the main results in the theory of conformal mapping of domains with variable boundaries; obtained by C. Carathéodory [1].

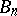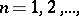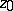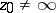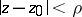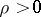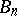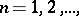Let , be a sequence of simply-connected domains of the -plane containing a fixed point , . If there exists a disc , , belonging to all , then the kernel of the sequence , with respect to is the largest domain 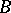containing 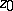and such that for each compact set 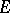belonging to there is an 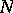such that 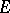belongs to 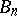for all 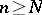. A largest domain is one which contains any other domain having the same property. If there is no such a disc, then by the kernel 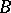of the sequence 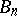, 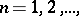one means the point 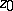(in this case one says that the sequence 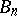, 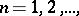has a degenerate kernel). A sequence of domains 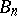, converges to a kernel 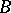if any subsequence of has as its kernel.

Carathéodory's theorem. Suppose that one is given a sequence of functions 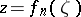, , , 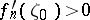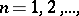that are regular and univalent in the disc 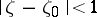and that map this disc onto the domains 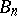, respectively. Then in order that the sequence 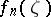, 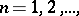converges in the disc 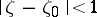to a finite function 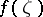, it is necessary and sufficient that the sequence 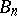, 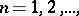converges to a kernel 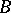which is either the point 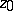or a domain containing more than one boundary point. Moreover, the convergence is uniform on compact sets in the interior of the disc 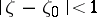. 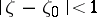If the limit function , then it maps the disc univalently onto 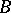, and the inverse functions 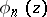, are uniformly convergent on compact sets in the interior of 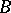to the inverse function 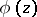of .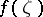

The question of the convergence of univalent functions in multiply-connected domains is considered analogously. One such theorem is given below for unbounded domains. Let 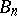, 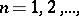be a sequence of domains in the -plane containing some fixed neighbourhood of 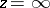. Then the kernel of the sequence 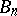, with respect to 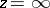is the largest domain 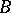containing 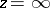and such that any closed subdomain of it is a subset of all 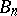from some onwards. Convergence of the sequence 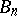, 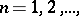to the kernel 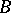is defined as before. The following theorem holds [2]. Let 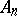, 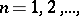be a sequence of domains in the -plane containing 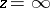and converging to a kernel 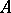, and suppose that the functions 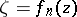, 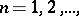map them univalently onto corresponding domains 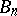containing 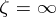; 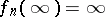, , 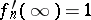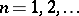. Then in order that the sequence , 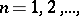converges uniformly on compact sets in the interior of 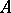to a univalent function 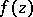, it is necessary and sufficient that the sequence 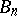, 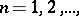possesses a kernel 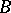and converges to it. In this case 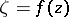maps 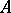univalently onto .

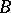It is possible to give other theorems on the convergence of a sequence of univalent functions, in dependence of the method of normalizing them (see [2]).

References

[1]	C. Carathéodory, "Untersuchungen über die konformen Abbildungen von festen und veränderlichen Gebieten" Math. Ann. , 72 (1912) pp. 107–144
[2]	G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian)

References

[a1]	P.L. Duren, "Univalent functions" , Springer (1983) pp. Chapt. 3