Carathéodory-Fejér problem
The problem of extending a polynomial in  to a power series representing a regular function in the disc
to a power series representing a regular function in the disc 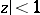 which realizes the least value of the supremum of the modulus on the disc
which realizes the least value of the supremum of the modulus on the disc 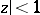 in the class of all regular functions in the unit disc having the given polynomial as initial segment of the MacLaurin series. The solution to this problem is given by the following theorem.
in the class of all regular functions in the unit disc having the given polynomial as initial segment of the MacLaurin series. The solution to this problem is given by the following theorem.
Carathéodory–Fejér theorem [1]. Let
 |
be a given polynomial, 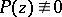 . There exists a unique rational function
. There exists a unique rational function 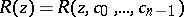 of the form
of the form
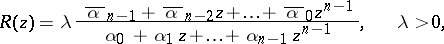 |
regular in the unit disc and having 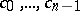 as the first
as the first  coefficients of its MacLaurin expansion. This function, and only this, realizes the minimum value of
coefficients of its MacLaurin expansion. This function, and only this, realizes the minimum value of
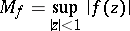 |
in the class of all regular functions 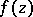 in the unit disc of the form
in the unit disc of the form
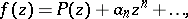 |
and this minimum value is 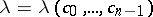 .
.
The number 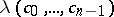 is equal to the largest positive root of the following equation of degree
is equal to the largest positive root of the following equation of degree 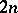 :
:
 |
If 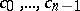 are real, then
are real, then 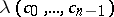 is the largest of the absolute values of the roots of the following equation of degree
is the largest of the absolute values of the roots of the following equation of degree  :
:
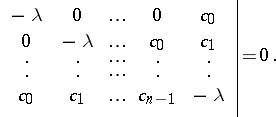 |
References
| [1] | C. Carathéodory, L. Fejér, "Ueber den Zusammenhang der Extremen von harmonischen Funktionen mit ihren Koeffizienten und den Picard–Landau'schen Satz" Rend. Circ. Mat. Palermo , 32 (1911) pp. 218–239 |
| [2] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
Carathéodory-Fejér problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Carath%C3%A9odory-Fej%C3%A9r_problem&oldid=23218