on roots
A theorem which establishes relations between the roots and the coefficients of a polynomial. Let  be a polynomial of degree
be a polynomial of degree  with coefficients from some field and with leading coefficient 1. The polynomial
with coefficients from some field and with leading coefficient 1. The polynomial  splits over a field containing all the roots of
splits over a field containing all the roots of  (e.g. over the splitting field of
(e.g. over the splitting field of  , cf. Splitting field of a polynomial) into linear factors:
, cf. Splitting field of a polynomial) into linear factors:
where  are the roots of
are the roots of  ,
, 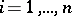 . Viète's theorem asserts that the following relations (Viète's formulas) hold:
. Viète's theorem asserts that the following relations (Viète's formulas) hold:
F. Viète [1] proved this relation for all  , but for positive roots only; the general form of Viète's theorem was established by A. Girard [2].
, but for positive roots only; the general form of Viète's theorem was established by A. Girard [2].
References
| [1] | F. Viète, "Opera mathematica" F. van Schouten (ed.) , Leiden (1646) |
| [2] | A. Girard, "Invention nouvelle en l'algèbre" , Bierens de Haan , Leiden (1884) (Reprint) |
A polynomial with leading coefficient 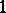 is called monic. Up to sign, the expressions for
is called monic. Up to sign, the expressions for 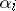 in Viète's theorem are nowadays known as the (elementary) symmetric polynomials (of
in Viète's theorem are nowadays known as the (elementary) symmetric polynomials (of  variables; cf. Symmetric polynomial).
variables; cf. Symmetric polynomial).
Viète's name is sometimes spelled Vièta: Vièta theorem.
References
| [a1] | B.L. van der Waerden, "Algebra" , 1 , Springer (1967) (Translated from German) |
How to Cite This Entry:
Viète theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vi%C3%A8te_theorem&oldid=23101
This article was adapted from an original article by V.N. Remeslennikov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article be a polynomial of degree
be a polynomial of degree  with coefficients from some field and with leading coefficient 1. The polynomial
with coefficients from some field and with leading coefficient 1. The polynomial  splits over a field containing all the roots of
splits over a field containing all the roots of  (e.g. over the splitting field of
(e.g. over the splitting field of  , cf. Splitting field of a polynomial) into linear factors:
, cf. Splitting field of a polynomial) into linear factors:
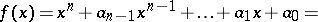
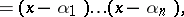
 are the roots of
are the roots of  ,
, 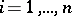 . Viète's theorem asserts that the following relations (Viète's formulas) hold:
. Viète's theorem asserts that the following relations (Viète's formulas) hold:
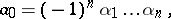
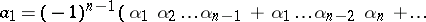
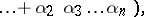

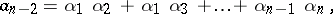

 , but for positive roots only; the general form of Viète's theorem was established by A. Girard [2].
, but for positive roots only; the general form of Viète's theorem was established by A. Girard [2].
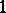 is called monic. Up to sign, the expressions for
is called monic. Up to sign, the expressions for 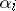 in Viète's theorem are nowadays known as the (elementary) symmetric polynomials (of
in Viète's theorem are nowadays known as the (elementary) symmetric polynomials (of  variables; cf. Symmetric polynomial).
variables; cf. Symmetric polynomial).