Szegö quadrature
Szegö quadrature formulas are the analogues on the unit circle  in the complex plane of the Gauss quadrature formulas on an interval (cf. also Gauss quadrature formula). They approximate the integral
in the complex plane of the Gauss quadrature formulas on an interval (cf. also Gauss quadrature formula). They approximate the integral
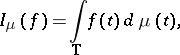 |
where  and
and  is a positive measure on
is a positive measure on  , by a quadrature formula of the form
, by a quadrature formula of the form
 |
One cannot take the zeros of the Szegö polynomials  as nodes (as in Gaussian formulas), because these are all in the open unit disc
as nodes (as in Gaussian formulas), because these are all in the open unit disc  (cf. also Szegö polynomial). Therefore, the para-orthogonal polynomials are introduced as
(cf. also Szegö polynomial). Therefore, the para-orthogonal polynomials are introduced as  , where
, where  and
and 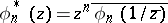 . These are orthogonal to
. These are orthogonal to 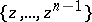 and have
and have  simple zeros, which are on
simple zeros, which are on 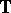 . The Szegö quadrature formula then takes as nodes the zeros
. The Szegö quadrature formula then takes as nodes the zeros 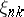 ,
, 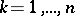 , of
, of 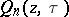 , and as weights the Christoffel numbers
, and as weights the Christoffel numbers
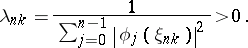 |
The result is a quadrature formula with a maximal domain of validity in the set of Laurent polynomials, i.e., the formula is exact for all trigonometric polynomials in 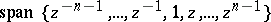 , a space of dimension
, a space of dimension 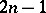 , which is the maximal dimension possible with a quadrature formula of this form.
, which is the maximal dimension possible with a quadrature formula of this form.
The Szegö quadrature formulas were introduced in [a2]. The underlying ideas have been generalized from polynomials to rational functions. See [a1].
References
| [a1] | A. Bultheel, P. González-Vera, E. Hendriksen, O. Njåstad, "Quadrature and orthogonal rational functions" J. Comput. Appl. Math. , 127 (2001) pp. 67–91 (Invited paper) |
| [a2] | W.B. Jones, O. Njåstad, W.J. Thron, "Moment theory, orthogonal polynomials, quadrature and continued fractions associated with the unit circle" Bull. London Math. Soc. , 21 (1989) pp. 113–152 |
Szegö quadrature. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Szeg%C3%B6_quadrature&oldid=23067