Skolem-Mahler-Lech theorem
A recurrence sequence  of order
of order  is a solution to a linear homogeneous recurrence relation with constant coefficients
is a solution to a linear homogeneous recurrence relation with constant coefficients
 |
Thus, the generating function  of a recurrence is a rational function
of a recurrence is a rational function  where
where  , say; the polynomial
, say; the polynomial  of degree less than
of degree less than  is determined by the initial values
is determined by the initial values  . If so, the distinct complex numbers
. If so, the distinct complex numbers 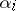 are called the roots of the recurrence, and the
are called the roots of the recurrence, and the 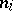 their multiplicities. It follows that the
their multiplicities. It follows that the  are given by a generalized power sum
are given by a generalized power sum  (
( ); the polynomial coefficients
); the polynomial coefficients 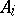 are respectively of degree
are respectively of degree  .
.
The theorem of Skolem–Mahler–Lech asserts that if a recurrence (equivalently, a generalized power sum) has infinitely many zeros, then those zeros occur periodically. That is, given a power series  representing a rational function with infinitely many zero Taylor coefficients, the set
representing a rational function with infinitely many zero Taylor coefficients, the set  is a finite union of complete arithmetic progressions (cf. Arithmetic progression), plus (a pre-period of) finitely many isolated zeros. By virtue of Ritt's quotient theorem [a6], it is equivalent that an infinitude of integer zeros of a complex exponential polynomial
is a finite union of complete arithmetic progressions (cf. Arithmetic progression), plus (a pre-period of) finitely many isolated zeros. By virtue of Ritt's quotient theorem [a6], it is equivalent that an infinitude of integer zeros of a complex exponential polynomial  is accounted for by it being divisible (in the ring of exponential polynomials) by functions
is accounted for by it being divisible (in the ring of exponential polynomials) by functions  .
.
Skolem's argument was generalized by K. Mahler to algebraic number fields, and eventually to arbitrary fields of characteristic zero by C. Lech and by Mahler. The elegant argument of J.W.S. Cassels [a1] bypasses the technical complications in the chain of successive generalizations. In brief, one observes that there are rational primes 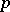 so that (technically, after embedding the data in the field
so that (technically, after embedding the data in the field  of
of 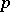 -adic rationals) one has
-adic rationals) one has  for each root. Then, for
for each root. Then, for  , each of the
, each of the  different
different 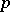 -adic exponential polynomials
-adic exponential polynomials  is a
is a  -adic analytic function in the disc
-adic analytic function in the disc 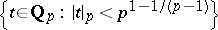 . It follows that if any one of these functions has infinitely many zeros (it turns out, as few as
. It follows that if any one of these functions has infinitely many zeros (it turns out, as few as  zeros [a3]) in the unit disc, then it must vanish identically, yielding the theorem with arithmetic progressions with common difference
zeros [a3]) in the unit disc, then it must vanish identically, yielding the theorem with arithmetic progressions with common difference  . It follows that a recurrence sequence can have infinitely many zeros only if it is degenerate, that is, some quotient
. It follows that a recurrence sequence can have infinitely many zeros only if it is degenerate, that is, some quotient  of its distinct roots is a root of unity.
of its distinct roots is a root of unity.
The theorem is provable without visible appeal to 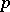 -adic analysis [a2]. But a generalization, whereby if two recurrence sequences have infinitely many elements in common then they coincide along certain of their arithmetic subprogressions (see [a4]), as yet, (1996) relies on a
-adic analysis [a2]. But a generalization, whereby if two recurrence sequences have infinitely many elements in common then they coincide along certain of their arithmetic subprogressions (see [a4]), as yet, (1996) relies on a 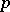 -adic generalization of Schmidt's subspace theorem. A different generalization, Shapiro's conjecture, according to which two exponential polynomials with infinitely many complex common zeros must have a common exponential polynomial factor, is still (1996) mostly conjecture [a5].
-adic generalization of Schmidt's subspace theorem. A different generalization, Shapiro's conjecture, according to which two exponential polynomials with infinitely many complex common zeros must have a common exponential polynomial factor, is still (1996) mostly conjecture [a5].
A general reference surveying this and other relevant material is [a7].
References
| [a1] | J.W.S. Cassels, "An embedding theorem for fields" Bull. Austral. Math. Soc. , 14 (1976) pp. 193–198 (Addendum: 14 (1976), 479–480) |
| [a2] | G. Hansel, "Une démonstration simple du théorème de Skolem–Mahler–Lech" Theor. Comput. Sci. , 43 (1986) pp. 91–98 |
| [a3] | A.J. van der Poorten, R.S. Rumely, "Zeros of  -adic exponential polynomials II" J. London Math. Soc. (2) , 36 (1987) pp. 1–15 -adic exponential polynomials II" J. London Math. Soc. (2) , 36 (1987) pp. 1–15 |
| [a4] | A.J. van der Poorten, H.-P. Schlickewei, "Additive relations in fields" J. Austral. Math. Soc. , 51 (1991) pp. 154–170 |
| [a5] | A.J. van der Poorten, R. Tijdeman, "On common zeros of exponential polynomials" L'Enseign. Math.  Série , 21 (1975) pp. 57–67 Série , 21 (1975) pp. 57–67 |
| [a6] | J.F. Ritt, "On the zeros of exponential polynomials" Trans. Amer. Math. Soc. , 31 (1929) pp. 680–686 |
| [a7] | A.J. van der Poorten, "Some facts that should be better known; especially about rational functions" R.A. Mollin (ed.) , Number Theory and Applications , NATO ASI , Kluwer Acad. Publ. (1989) pp. 497–528 |
Skolem-Mahler-Lech theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Skolem-Mahler-Lech_theorem&oldid=23027