Möbius inversion
A method for inverting sums over partially ordered sets (or posets; cf. also Partially ordered set). The theory of Möbius inversion matured in the classic paper [a4] of G.-C. Rota and is a cornerstone of algebraic combinatorics (cf. also Combinatorics).
Let 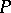 be a locally finite partially ordered set, that is, a poset in which every interval
be a locally finite partially ordered set, that is, a poset in which every interval 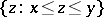 is finite. The Möbius function
is finite. The Möbius function 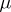 of
of 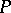 is the function on pairs of elements in
is the function on pairs of elements in 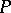 defined by the following conditions:
defined by the following conditions: 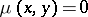 if
if 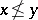 ,
, 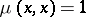 for all
for all  , and the recursive relation
, and the recursive relation
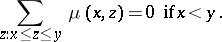 |
When 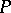 is finite, the function value
is finite, the function value 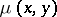 is the
is the 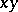 -entry in the inverse of the incidence matrix of the partial order relation on
-entry in the inverse of the incidence matrix of the partial order relation on 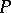 .
.
Let 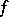 ,
, 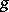 be functions defined from
be functions defined from 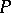 to a commutative ring
to a commutative ring 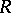 with unity. The Möbius inversion formula states:
with unity. The Möbius inversion formula states:
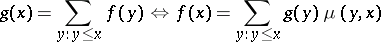 |
or, dually,
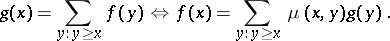 |
For the Boolean algebra 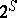 of all subsets of a set
of all subsets of a set 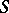 ,
, 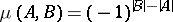 when
when 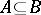 . When
. When 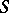 is thought of as a set of "properties" , the Möbius inversion formula yields the principle of inclusion-exclusion (cf. Inclusion-and-exclusion principle).
is thought of as a set of "properties" , the Möbius inversion formula yields the principle of inclusion-exclusion (cf. Inclusion-and-exclusion principle).
When 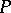 is the distributive lattice of positive integers ordered by divisibility, the Möbius function
is the distributive lattice of positive integers ordered by divisibility, the Möbius function 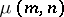 equals
equals  unless
unless 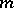 divides
divides  and
and 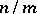 is square-free, in which case it equals
is square-free, in which case it equals 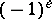 , where
, where  is the number of primes in the prime factorization of
is the number of primes in the prime factorization of 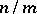 . The classical or number-theoretic Möbius inversion formula states:
. The classical or number-theoretic Möbius inversion formula states:
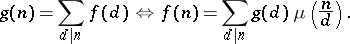 |
For example, this yields the following formula for the Euler totient function 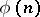 , the number of positive integers not exceeding
, the number of positive integers not exceeding  that are relatively prime to
that are relatively prime to  (cf. also Euler function):
(cf. also Euler function):
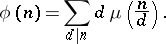 |
The Möbius function satisfies many identities. Four often-used identities are:
a) The P. Hall identity:
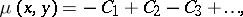 |
where 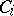 is the number of (strict) chains
is the number of (strict) chains 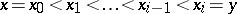 with
with 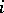 links starting at
links starting at  and ending at
and ending at 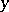 (cf. also Chain).
(cf. also Chain).
b) The Weisner theorem: Let 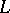 be a finite lattice with minimum
be a finite lattice with minimum  . If
. If  and
and 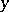 are elements of
are elements of 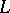 such that
such that 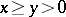 , then
, then
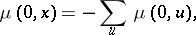 |
the sum ranging over all elements  such that
such that 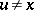 and
and 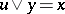 .
.
c) The Crapo complementation theorem: An element 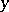 is a complement of an element
is a complement of an element  in a lattice
in a lattice 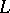 with minimum
with minimum  and maximum
and maximum 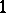 if
if 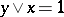 and
and 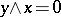 . For any element
. For any element  in a finite lattice
in a finite lattice 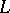 ,
,
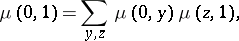 |
the sum ranging over all pairs 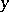 and
and  such that
such that 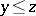 and both
and both 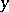 and
and  are complements of
are complements of  .
.
d) The Boolean expansion lemma: If 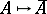 is a closure operator on a set
is a closure operator on a set 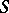 (cf. also Closure space), then for a closed set
(cf. also Closure space), then for a closed set 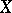 in the lattice of closed sets,
in the lattice of closed sets,
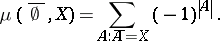 |
The Boolean expansion lemma is a special case of the Galois connection theorem. It is also a special case of the cross-cut theorem. A cross-cut 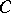 in a finite lattice
in a finite lattice 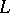 is a set of elements of
is a set of elements of 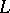 satisfying:
satisfying:
1) 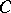 does not contain the minimum
does not contain the minimum  or the maximum
or the maximum 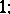
2) no pair of elements of 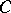 is comparable;
is comparable;
3) any maximal chain from  to
to 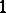 has non-empty intersection with
has non-empty intersection with 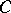 . A subset
. A subset 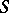 of elements of
of elements of  is spanning if both the join of all the elements in
is spanning if both the join of all the elements in 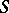 is
is  and the meet of all the elements in
and the meet of all the elements in  is
is  . If
. If 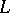 is a finite lattice with more than two elements and
is a finite lattice with more than two elements and 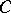 is a cross-cut in
is a cross-cut in 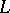 , then
, then
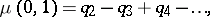 |
where 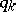 is the number of spanning subsets of
is the number of spanning subsets of 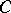 with
with 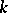 elements.
elements.
Besides order-theoretic, homological and counting proofs of these results, there are also proofs using the Möbius algebra, a generalization of the Burnside algebra of a group.
Much work has been done on calculating Möbius functions of specific partially ordered sets. For example, if 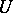 and
and 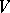 are subspaces in the lattice of subspaces of a finite-dimensional vector space over a finite field of order
are subspaces in the lattice of subspaces of a finite-dimensional vector space over a finite field of order 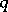 and
and 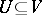 , then
, then
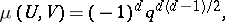 |
where 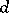 is the difference
is the difference 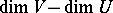 .
.
There are many results relating structural properties and properties of the Möbius function. Two examples follow. For an element  in a lattice,
in a lattice, 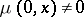 only if the element
only if the element  is a join of atoms. (Atoms are elements covering the minimum
is a join of atoms. (Atoms are elements covering the minimum  ; cf. also Atom.) If
; cf. also Atom.) If 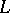 is a finite lattice in which
is a finite lattice in which 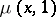 is non-zero for all elements
is non-zero for all elements  , then there exists a bijection
, then there exists a bijection 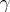 from
from 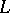 to itself such that for every
to itself such that for every  ,
, 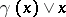 is the maximum
is the maximum 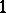 .
.
Möbius functions occur in many proofs. For example, they are heavily used in the original proof of Dilworth's theorem that in a finite modular lattice, the number of elements covering 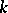 or fewer elements equals the number of elements covered by
or fewer elements equals the number of elements covered by 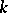 or fewer elements, and its extension, that the incidence matrix or combinatorial Radon transform between these two sets of elements is invertible.
or fewer elements, and its extension, that the incidence matrix or combinatorial Radon transform between these two sets of elements is invertible.
The Möbius function has a homological interpretation. The value  for a partially ordered set
for a partially ordered set 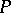 with minimum
with minimum  and maximum
and maximum 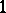 is the Euler characteristic of the order complex of
is the Euler characteristic of the order complex of 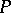 , the simplicial complex whose simplices are the chains of
, the simplicial complex whose simplices are the chains of 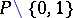 , the partially ordered set
, the partially ordered set 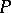 with
with  and
and 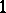 deleted. Because polytopes are topologically spheres, this yields the following theorem. If
deleted. Because polytopes are topologically spheres, this yields the following theorem. If 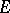 and
and 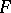 are faces in the face lattice of a polytope and
are faces in the face lattice of a polytope and 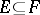 , then
, then 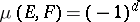 , where
, where 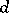 is the difference
is the difference 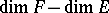 . Taking the nerve of a covering of the order complex (cf. also Nerve of a family of sets), one obtains a homology based on a cross-cut and the cross-cut theorem.
. Taking the nerve of a covering of the order complex (cf. also Nerve of a family of sets), one obtains a homology based on a cross-cut and the cross-cut theorem.
The homological interpretation is especially interesting for a geometric lattice 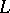 . In this case, the only non-trivial homology groups (cf. Homology group) are
. In this case, the only non-trivial homology groups (cf. Homology group) are 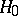 and
and 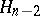 , where
, where  is the rank of
is the rank of 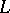 , and
, and 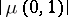 is the rank or dimension of the top homology group
is the rank or dimension of the top homology group 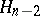 . Rota has proved the following sign theorem: If
. Rota has proved the following sign theorem: If  is a rank-
is a rank-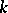 flat in a geometric lattice, then
flat in a geometric lattice, then 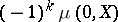 is positive. Indeed,
is positive. Indeed, 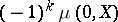 counts certain subsets in the broken-circuit complex defined by H. Whitney.
counts certain subsets in the broken-circuit complex defined by H. Whitney.
The characteristic polynomial 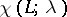 of a ranked partially ordered set
of a ranked partially ordered set 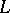 is the polynomial
is the polynomial
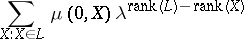 |
in the variable 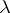 . With simple modifications, one can obtain from the characteristic polynomial of a geometric lattice the Poincaré polynomial of an arrangement of hyperplanes and the chromatic polynomial of a graph (cf. also Graph colouring). The characteristic polynomial is an essential tool in the critical problem for matroids (cf. also Matroid). Related to the characteristic polynomial is the Eulerian function
. With simple modifications, one can obtain from the characteristic polynomial of a geometric lattice the Poincaré polynomial of an arrangement of hyperplanes and the chromatic polynomial of a graph (cf. also Graph colouring). The characteristic polynomial is an essential tool in the critical problem for matroids (cf. also Matroid). Related to the characteristic polynomial is the Eulerian function 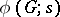 of a finite group
of a finite group 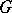 , defined to be the Dirichlet polynomial
, defined to be the Dirichlet polynomial
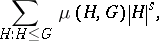 |
where the sum ranges over all subgroups in the subgroup lattice of 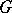 . When
. When  is a positive integer,
is a positive integer, 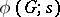 is the number of
is the number of  -tuples of group elements whose underlying set generate
-tuples of group elements whose underlying set generate 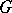 .
.
The Möbius invariant 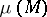 of a matroid
of a matroid 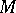 is the integer
is the integer 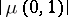 with
with 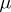 calculated in its lattice of flats if
calculated in its lattice of flats if 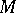 has no loops, and
has no loops, and  otherwise. Except when the element
otherwise. Except when the element  is an isthmus,
is an isthmus, 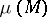 satisfies the relation
satisfies the relation
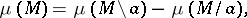 |
where 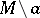 is
is 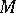 with
with  deleted and
deleted and 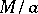 is
is  contracted at
contracted at  . The triple
. The triple 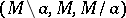 is an analogue of a short exact sequence (cf. also Exact sequence). Many other invariants (including the characteristic polynomial) satisfy contraction-and-deletion relations. In addition, inductive arguments involving contractions and deletions are often used in proofs.
is an analogue of a short exact sequence (cf. also Exact sequence). Many other invariants (including the characteristic polynomial) satisfy contraction-and-deletion relations. In addition, inductive arguments involving contractions and deletions are often used in proofs.
References
| [a1] | M. Barnabei, A. Brini, G.-C. Rota, "Theory of Möbius functions" Russian Math. Surveys , 3 (1986) pp. 135–188 |
| [a2] | A. Björner, "Homology and shellability of matroids and geometric lattices" N.L. White (ed.) , Matroid Applications , Cambridge Univ. Press (1992) pp. 226–283 |
| [a3] | J.P.S. Kung, "Radon transforms in combinatorics and lattice theory" I. Rival (ed.) , Combinatorics and Ordered Sets , Amer. Math. Soc. (1986) pp. 33–74 |
| [a4] | G.-C. Rota, "On the foundations of combinatorial theory I: Theory of Möbius functions" Z. Wahrsch. Verw. Gebiete , 2 (1964) pp. 340–368 |
Möbius inversion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=M%C3%B6bius_inversion&oldid=22813