Mann-Whitney test
A statistical test for testing the hypothesis 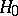 of homogeneity of two samples
of homogeneity of two samples 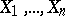 and
and 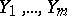 , all
, all 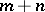 elements of which are mutually independent and have continuous distributions. This test, suggested by H.B. Mann and D.R. Whitney [1], is based on the statistic
elements of which are mutually independent and have continuous distributions. This test, suggested by H.B. Mann and D.R. Whitney [1], is based on the statistic
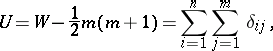 |
where  is the statistic of the Wilcoxon test intended for testing the same hypothesis, equal to the sum of the ranks of the elements of the second sample among the pooled order statistics (cf. Order statistic), and
is the statistic of the Wilcoxon test intended for testing the same hypothesis, equal to the sum of the ranks of the elements of the second sample among the pooled order statistics (cf. Order statistic), and
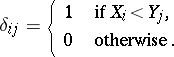 |
Thus, 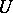 counts the number of cases when the elements of the second sample exceed elements of the first sample. It follows from the definition of
counts the number of cases when the elements of the second sample exceed elements of the first sample. It follows from the definition of 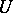 that if
that if 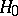 is true, then
is true, then
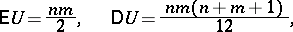 | (*) |
and, in addition, this statistic has all the properties of the Wilcoxon statistic 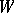 , including asymptotic normality with parameters (*).
, including asymptotic normality with parameters (*).
References
| [1] | H.B. Mann, D.R. Whitney, "On a test whether one of two random variables is statistically larger than the other" Ann. Math. Stat. , 18 (1947) pp. 50–60 |
Comments
Instead of Mann–Whitney test, the phrase 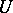 -test is also used.
-test is also used.
Mann-Whitney test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mann-Whitney_test&oldid=22789