Lindelöf hypothesis
From Encyclopedia of Mathematics
Revision as of 18:53, 24 March 2012 by Ulf Rehmann (talk | contribs) (moved Lindelöf hypothesis to Lindelof hypothesis: ascii title)
Lindelöf conjecture, on the behaviour of the Riemann 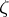 -function
-function
For any 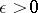 ,
,
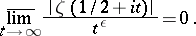 |
It was stated by E. Lindelöf [1]. The Lindelöf conjecture is equivalent to the assertion that for a fixed 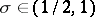 the number of zeros of
the number of zeros of 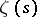 that lie in the domain
that lie in the domain 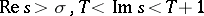 is
is 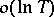 . The Lindelöf conjecture is therefore a consequence of the Riemann conjecture on the zeros of
. The Lindelöf conjecture is therefore a consequence of the Riemann conjecture on the zeros of 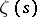 (cf. Riemann hypotheses). It is known (1982) that
(cf. Riemann hypotheses). It is known (1982) that
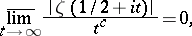 |
where  is a constant such that
is a constant such that 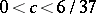 .
.
There is a generalization of the Lindelöf conjecture to Dirichlet 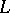 -functions: For any
-functions: For any 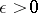 ,
,
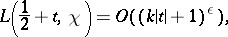 |
where 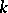 is the modulus of the character
is the modulus of the character 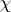 .
.
References
| [1] | E. Lindelöf, "Le calcul des résidus et ses applications à la théorie des fonctions" , Gauthier-Villars (1905) |
| [2] | E.C. Titchmarsh, "The theory of the Riemann zeta-function" , Oxford Univ. Press (1951) pp. Chapt. 13 |
Comments
References
| [a1] | A. Ivic, "The Riemann zeta-function" , Wiley (1985) |
How to Cite This Entry:
Lindelöf hypothesis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lindel%C3%B6f_hypothesis&oldid=22751
Lindelöf hypothesis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lindel%C3%B6f_hypothesis&oldid=22751
This article was adapted from an original article by S.M. Voronin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article