Lie-Kolchin theorem

A solvable subgroup of the group (where is a finite-dimensional vector space over an algebraically closed field) has a normal subgroup of index at most , where depends only on , such that in there is a flag that is invariant with respect to 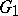. In other words, there is a basis in 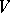in which the elements of are written as triangular matrices. If is a connected closed subgroup of 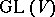in the Zariski topology, then ; in this case the Lie–Kolchin theorem is a generalization of Lie's theorem, which was proved by S. Lie for complex connected (in the Euclidean topology) solvable Lie groups (see Lie group, solvable; Lie theorem). This assertion can also be considered as a special case of Borel's fixed-point theorem (cf. Borel fixed-point theorem).

The following analogue of the Lie–Kolchin theorem is true for an arbitrary field: A solvable group of matrices contains a normal subgroup of finite index whose commutator subgroup is nilpotent.

The Lie–Kolchin theorem was proved by E.R. Kolchin [1] (for connected groups) and A.I. Mal'tsev [2] (in the general formulation). It is also sometimes called the Kolchin–Mal'tsev theorem.

References

[1]	E.R. Kolchin, "Algebraic matrix groups and the Picard–Vessiot theory of homogeneous linear ordinary differential equations" Ann. of Math. (2) , 49 (1948) pp. 1–42
[2]	A.I. [A.I. Mal'tsev] Mal'Avcev, "On certain classes of infinite soluble groups" Transl. Amer. Math. Soc. (2) , 2 (1956) pp. 1–21 Mat. Sb. , 28 (1951) pp. 567–588
[3]	M.I. Kargapolov, J.I. [Yu.I. Merzlyakov] Merzljakov, "Fundamentals of the theory of groups" , Springer (1979) (Translated from Russian)

Comments

In Western literature the Lie–Kolchin theorem usually designates the more restricted version about connected closed subgroups of .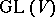

For the role of the Lie–Kolchin theorem in the Galois theory for ordinary linear differential equations see [a1].

References

[a1]	I. Kaplansky, "An introduction to differential algebra" , Hermann (1957)
[a2]	J.E. Humphreys, "Linear algebraic groups" , Springer (1975) pp. Sect. 35.1
[a3]	A. Borel, "Linear algebraic groups" , Benjamin (1969) pp. 283ff