Kuratowski-Knaster fan
Knaster–Kuratowski fan
A totally disconnected set in the plane which becomes connected when just one point is added. Constructed by B. Knaster and C. Kuratowski [1] as follows. Let 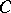 be the perfect Cantor set,
be the perfect Cantor set, 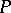 the subset of
the subset of 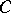 consisting of the points
consisting of the points 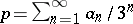 such that, beginning from some
such that, beginning from some  , the numbers
, the numbers 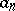 are either all zero or all equal to 2; and let
are either all zero or all equal to 2; and let 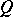 be the set of all the other points. Now, let
be the set of all the other points. Now, let  be the point on the plane with coordinates
be the point on the plane with coordinates 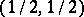 , and let
, and let 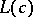 be the segment joining a variable point
be the segment joining a variable point  of
of 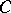 to the point
to the point  . Finally, let
. Finally, let 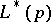 be the set of all points of
be the set of all points of 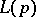 that have rational ordinates for
that have rational ordinates for  , and let
, and let 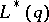 be the set of all points of
be the set of all points of 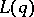 that have irrational ordinates for
that have irrational ordinates for 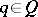 . Then
. Then
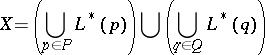 |
is connected, although 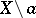 is totally disconnected, so that
is totally disconnected, so that 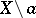 is a Knaster–Kuratowski fan.
is a Knaster–Kuratowski fan.
References
| [1] | B. Knaster, C. Kuratowski, "Sur les ensembles connexes" Fund. Math. , 2 (1921) pp. 206–255 |
Kuratowski-Knaster fan. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kuratowski-Knaster_fan&oldid=22689