Ivanov-Petrova metric
Let 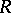 be the Riemann curvature tensor of a Riemannian manifold
be the Riemann curvature tensor of a Riemannian manifold 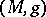 . If
. If 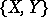 is an orthonormal basis for an oriented
is an orthonormal basis for an oriented  -plane
-plane 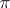 in the tangent space at a point
in the tangent space at a point 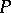 of
of 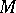 , let
, let 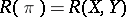 be the skew-symmetric curvature operator introduced by R. Ivanova and G. Stanilov [a3]. The Riemannian metric is said to be an Ivanov–Petrova metric if the eigenvalues of
be the skew-symmetric curvature operator introduced by R. Ivanova and G. Stanilov [a3]. The Riemannian metric is said to be an Ivanov–Petrova metric if the eigenvalues of 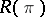 depend only on the point
depend only on the point 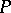 but not upon the particular
but not upon the particular  -plane in question.
-plane in question.
Example 1.
If 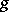 is a metric of constant sectional curvature
is a metric of constant sectional curvature 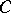 , then the group of local isometries acts transitively on the Grassmannian of oriented
, then the group of local isometries acts transitively on the Grassmannian of oriented  -planes and hence
-planes and hence 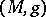 is Ivanov–Petrova. The eigenvalues of
is Ivanov–Petrova. The eigenvalues of 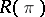 are
are 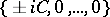 .
.
Example 2.
Let 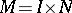 be a product manifold, where
be a product manifold, where 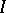 is a subinterval of
is a subinterval of 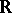 and where
and where 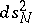 is a metric of constant sectional curvature
is a metric of constant sectional curvature 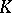 on
on 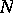 . Give
. Give 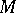 the metric
the metric
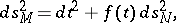 |
where 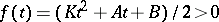 . One can then compute that the eigenvalues of
. One can then compute that the eigenvalues of  are
are 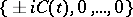 for
for 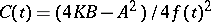 . Thus, this metric is Ivanov–Petrova.
. Thus, this metric is Ivanov–Petrova.
In Example 1, the eigenvalues of the skew-symmetric curvature operator are constant; in Example 2, the eigenvalues depend upon the point of the manifold. S. Ivanov and I. Petrova [a2] showed that in dimension 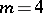 , any Riemannian manifold which is Ivanov–Petrova is locally isometric to one of the two metrics exhibited above. This result was later generalized [a4], [a1] to dimensions
, any Riemannian manifold which is Ivanov–Petrova is locally isometric to one of the two metrics exhibited above. This result was later generalized [a4], [a1] to dimensions 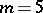 ,
, 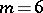 , and
, and 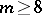 ; the case
; the case 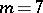 is exceptional and is still open (1998). Partial results in the Lorentzian setting have been obtained by T. Zhang [a5].
is exceptional and is still open (1998). Partial results in the Lorentzian setting have been obtained by T. Zhang [a5].
Let 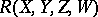 be a
be a 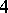 -tensor on
-tensor on 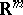 which defines a corresponding curvature operator
which defines a corresponding curvature operator 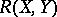 . If
. If 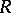 satisfies the identities,
satisfies the identities,
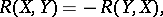 |
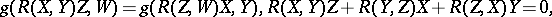 |
then 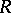 is said to be an algebraic curvature tensor. The algebraic curvature tensors which are Ivanov–Petrova have also been classified; they are known to have rank at most
is said to be an algebraic curvature tensor. The algebraic curvature tensors which are Ivanov–Petrova have also been classified; they are known to have rank at most  in all dimensions except
in all dimensions except 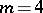 and
and 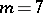 , and have the form
, and have the form
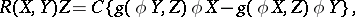 |
where 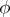 is an isometry with
is an isometry with 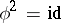 . Note that in dimension
. Note that in dimension 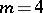 , there is an algebraic curvature tensor which is Ivanov–Petrova, has rank
, there is an algebraic curvature tensor which is Ivanov–Petrova, has rank 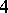 and which is constructed using the quaternions; up to scaling and change of basis it is unique and the non-zero entries (up to the usual curvature symmetries) are given by:
and which is constructed using the quaternions; up to scaling and change of basis it is unique and the non-zero entries (up to the usual curvature symmetries) are given by:
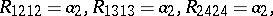 |
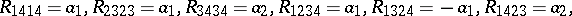 |
where 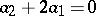 . The situation in dimension
. The situation in dimension 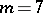 is open (1998).
is open (1998).
References
| [a1] | P. Gilkey, J.V. Leahy, H. Sadofsky, "Riemannian manifolds whose skew-symmetric curvature operator has constant eigenvalues" Indiana J. (to appear) |
| [a2] | S. Ivanov, I. Petrova, "Riemannian manifold in which the skew-symmetric curvature operator has pointwise constant eigenvalues" Geom. Dedicata , 70 (1998) pp. 269–282 |
| [a3] | R. Ivanova, G. Stanilov, "A skew-symmetric curvature operator in Riemannian geometry" M. Behara (ed.) R. Fritsch (ed.) R. Lintz (ed.) , Symposia Gaussiana, Conf. A (1995) pp. 391–395 |
| [a4] | P. Gilkey, "Riemannian manifolds whose skew-symmetric curvature operator has constant eigenvalues II" , Proc. Diff. Geom. Symp. (Brno, 1998) (to appear) |
| [a5] | T. Zhang, "Manifolds with indefinite metrics whose skew symmetric curvature operator has constant eigenvalues" PhD Thesis Univ. Oregon (2000) |
Ivanov-Petrova metric. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ivanov-Petrova_metric&oldid=22605