Hille-Tamarkin operator

Let 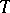be an integral operator from 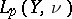into 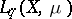, i.e., there exists a 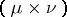-measurable functi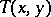on on 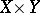such that 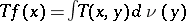a.e. on 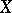. Then 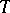is called a Hille–Tamarkin operator if

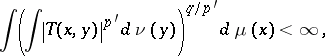where 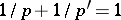. By taking 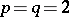one obtains the class of Hilbert–Schmidt operators (cf. Hilbert–Schmidt operator). Replacing 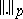, respectively 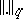, by arbitrary Banach function norms 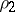, respectively 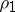, one obtains the class of Hille–Tamarkin operators between Banach function spaces (sometimes called integral operators of finite double norm, see [a1]). Under some mild hypotheses on the norms, one can show that Hille–Tamarkin operators have rather strong compactness properties (see [a2]).

References

[a1]	A.C. Zaanen, "Riesz spaces" , II , North-Holland (1983)
[a2]	A.R. Schep, "Compactness properties of Carleman and Hille–Tamarkin operators" Canad. J. Math. , 37 (1985) pp. 921–933