Grötzsch theorems
Various results on conformal and quasi-conformal mappings obtained by H. Grötzsch . He developed the strip method, which is the first general form of the method of conformal moduli (cf. Extremal metric, method of the; Strip method (analytic functions)), and used it in his systematic study of a large number of extremal problems of conformal mapping of multiply-connected (including infinitely-connected) domains, including the problems of the existence, uniqueness and geometric properties of extremal mappings. A few of the simpler Grötzsch theorems are presented below.
Of all univalent conformal mappings 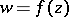 of a given annulus
of a given annulus 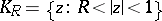 under which the unit circle
under which the unit circle 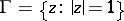 is mapped onto itself, the maximum diameter of the image of the circle
is mapped onto itself, the maximum diameter of the image of the circle 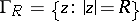 is attained if and only if the boundary component
is attained if and only if the boundary component 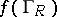 is a rectilinear segment with its centre at the point
is a rectilinear segment with its centre at the point 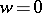 . A similar result is valid for multiply-connected domains.
. A similar result is valid for multiply-connected domains.
Out of all univalent conformal mappings 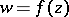 of a given multiply-connected domain
of a given multiply-connected domain 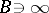 with expansion
with expansion 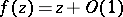
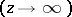 at infinity and normalization
at infinity and normalization 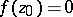 at a given point
at a given point 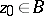 , the maximum of
, the maximum of 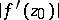 , and the maximum (minimum) of
, and the maximum (minimum) of 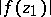 at a given point
at a given point 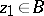 ,
, 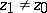 , are attained only on mappings that map each boundary component of
, are attained only on mappings that map each boundary component of 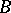 , respectively, to an arc of a circle with centre at the point
, respectively, to an arc of a circle with centre at the point 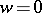 , or to an arc of an ellipse (hyperbola) with foci at the points
, or to an arc of an ellipse (hyperbola) with foci at the points 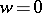 and
and 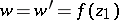 . In each one of these problems the extremal mapping exists and is unique. In this class of mappings, for a given
. In each one of these problems the extremal mapping exists and is unique. In this class of mappings, for a given 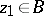 , the disc
, the disc
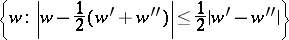 |
is the range of the function 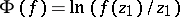 . Each boundary point of this disc is a value of
. Each boundary point of this disc is a value of 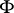 on a unique mapping in the class under study with specific geometric properties.
on a unique mapping in the class under study with specific geometric properties.
Grötzsch was the first to propose a form of representation of a quasi-conformal mapping, and to apply to such a mappings many extremal results which he had formerly obtained for conformal mappings.
References
| [1a] | H. Grötzsch, "Ueber die Verzerrung bei schlichter konformer Abbildung mehrfach zusammenhängender Bereiche I" Ber. Verh. Sächsisch. Akad. Wiss. Leipzig. Math.-Naturwiss. Kl. , 81 (1929) pp. 38–47 |
| [1b] | H. Grötzsch, "Ueber die Verzerrung bei schlichter konformer Abbildung mehrfach zusammenhängender Bereiche II" Ber. Verh. Sächsisch. Akad. Wiss. Leipzig. Math.-Naturwiss. Kl. , 81 (1929) pp. 217–221 |
| [1c] | H. Grötzsch, Ber. Verh. Sächsisch. Akad. Wiss. Leipzig. Math.-Naturwiss. Kl. , 82 (1930) pp. 69–80 |
| [1d] | H. Grötzsch, "Ueber die Verschiebung bei schlichter konformer Abbildung schlichter Bereiche II" Ber. Verh. Sächsisch. Akad. Wiss. Leipzig. Math.-Naturwiss. Kl. , 84 (1932) pp. 269–278 |
| [2] | J.A. Jenkins, "Univalent functions and conformal mappings" , Springer (1958) |
Comments
Grötzsch' theorems are distortion theorems.
Cf. also Grötzsch principle.
Grötzsch theorems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gr%C3%B6tzsch_theorems&oldid=22535