Gleason-Kahane-Żelazko theorem
Let 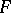 be a non-zero linear and multiplicative functional on a complex Banach algebra
be a non-zero linear and multiplicative functional on a complex Banach algebra 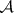 with a unit
with a unit  , and let
, and let 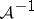 denote the set of all invertible elements of
denote the set of all invertible elements of 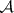 . Then
. Then  , and for any
, and for any  one has
one has 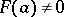 . A.M. Gleason [a1] and, independently, J.P. Kahane and W. Żelazko [a5], [a6] proved that the property characterizes multiplicative functionals: If
. A.M. Gleason [a1] and, independently, J.P. Kahane and W. Żelazko [a5], [a6] proved that the property characterizes multiplicative functionals: If 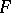 is a linear functional on a complex unital Banach algebra
is a linear functional on a complex unital Banach algebra 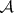 such that
such that 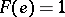 and
and 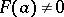 for
for 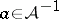 , then
, then 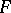 is multiplicative. Equivalently: a linear functional
is multiplicative. Equivalently: a linear functional 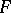 on a commutative complex unital Banach algebra
on a commutative complex unital Banach algebra 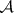 is multiplicative if and only if
is multiplicative if and only if 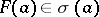 for all
for all 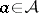 , where
, where 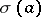 stands for the spectrum of
stands for the spectrum of  (cf. also Spectrum of an element). As there is a one-to-one correspondence between linear multiplicative functionals and maximal ideals, the theorem can also be phrased in the following way: A codimension-one subspace
(cf. also Spectrum of an element). As there is a one-to-one correspondence between linear multiplicative functionals and maximal ideals, the theorem can also be phrased in the following way: A codimension-one subspace 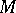 of a commutative complex unital Banach algebra
of a commutative complex unital Banach algebra 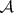 is an ideal if and only if each element of
is an ideal if and only if each element of 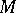 is contained in a non-trivial ideal. The theorem is not valid for real Banach algebras.
is contained in a non-trivial ideal. The theorem is not valid for real Banach algebras.
The Gleason–Kahane–Żelazko theorem has been extended into several directions:
1) If 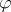 is non-constant entire function and
is non-constant entire function and 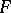 is a linear functional on a complex unital Banach algebra
is a linear functional on a complex unital Banach algebra  , such that
, such that 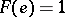 and
and 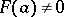 for
for 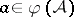 , then
, then 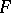 is multiplicative [a3].
is multiplicative [a3].
2) Let 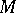 be a finite-codimensional subspace of the algebra
be a finite-codimensional subspace of the algebra 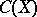 of all continuous complex-valued functions on a compact space
of all continuous complex-valued functions on a compact space 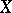 . If each element of
. If each element of 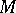 is equal to zero at some point of
is equal to zero at some point of 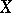 , then the functions from
, then the functions from 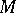 have a common zero in
have a common zero in 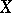 [a2]. It is not known if the analogous result is valid for all commutative unital Banach algebras.
[a2]. It is not known if the analogous result is valid for all commutative unital Banach algebras.
3) The assumption of linearity of the functional 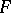 has been weakened, and the result has been extended to mappings between Banach and topological algebras.
has been weakened, and the result has been extended to mappings between Banach and topological algebras.
See [a4] for more information about the history, related problems, and further references.
References
| [a1] | A.M. Gleason, "A characterization of maximal ideals" J. d'Anal. Math. , 19 (1967) pp. 171–172 |
| [a2] | K. Jarosz, "Finite codimensional ideals in function algebras" Trans. Amer. Math. Soc. , 287 : 2 (1985) pp. 779–785 |
| [a3] | K. Jarosz, "Multiplicative functionals and entire functions II" Studia Math. , 124 : 2 (1997) pp. 193–198 |
| [a4] | K. Jarosz, "When is a linear functional multiplicative?" , Function Spaces: Proc. 3rd Conf. Function Spaces , Contemp. Math. , 232 , Amer. Math. Soc. (1999) |
| [a5] | J.-P. Kahane, W. Żelazko, "A characterization of maximal ideals in commutative Banach algebras" Studia Math. , 29 (1968) pp. 339–343 |
| [a6] | W. Żelazko, "A characterization of multiplicative linear functionals in complex Banach algebras" Studia Math. , 30 (1968) pp. 83–85 |
Gleason-Kahane-Żelazko theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gleason-Kahane-%C5%BBelazko_theorem&oldid=22509