Eilenberg-Moore algebra
From Encyclopedia of Mathematics
Revision as of 18:51, 24 March 2012 by Ulf Rehmann (talk | contribs) (moved Eilenberg–Moore algebra to Eilenberg-Moore algebra: ascii title)
Moore–Eilenberg algebra
Given a monad (or triple) 
in a category 
, a 
-algebra is a pair 
, 
, 
, such that the diagram
 |
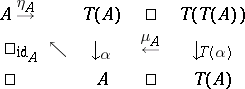commutes. Such a 
-algebra is also called an Eilenberg–Moore algebra. The forgetful functor from the category of Eilenberg–Moore algebras 
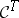to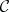 
has a left adjoint, exhibiting the monad 
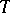as coming from a pair of adjoint functors (the Eilenberg–Moore construction).
See also Adjoint functor.
References
| [a1] | F. Borceux, "Handbook of categorical algebra: Categories and structures" , 2 , Cambridge Univ. Press (1994) pp. Chap. 4 |
How to Cite This Entry:
Eilenberg-Moore algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Eilenberg-Moore_algebra&oldid=22373
Eilenberg-Moore algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Eilenberg-Moore_algebra&oldid=22373
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article