De la Vallée-Poussin singular integral
From Encyclopedia of Mathematics
Revision as of 18:51, 24 March 2012 by Ulf Rehmann (talk | contribs) (moved De la Vallée-Poussin singular integral to De la Vallee-Poussin singular integral: ascii title)
An integral of the form
 |
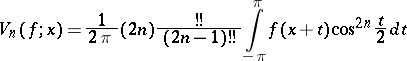(see also de la Vallée-Poussin summation method). The sequence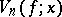 
converges uniformly to 
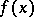for functions 
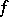which are continuous and 
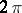-periodic on 
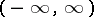[1]. If
 |
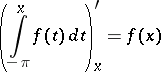at a point 
, then 
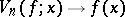as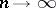 
. The following equality is valid [2]:
 |
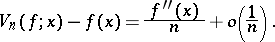References
| [1] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
| [2] | I.P. Natanson, "Constructive function theory" , 1 , F. Ungar (1964) (Translated from Russian) |
Comments
The notation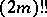 
stands for 
(
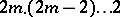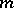terms), and 
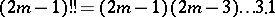(also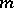 
terms). Thus,
 |
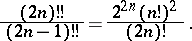How to Cite This Entry:
De la Vallée-Poussin singular integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=De_la_Vall%C3%A9e-Poussin_singular_integral&oldid=22329
De la Vallée-Poussin singular integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=De_la_Vall%C3%A9e-Poussin_singular_integral&oldid=22329
This article was adapted from an original article by P.P. Korovkin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article