Choquet-Kendall-Matheron theorem
A theorem characterizing the distribution of a random closed set in terms of the Choquet capacity functional [a1]. This theorem was established independently by D.G. Kendall [a2] and G. Matheron [a3] in their work on random closed sets.
Let 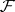 and
and 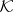 be the family of closed and compact subsets of
be the family of closed and compact subsets of 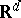 , respectively. The family
, respectively. The family 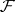 is endowed with the hit-or-miss topology, which is generated by
is endowed with the hit-or-miss topology, which is generated by
 |
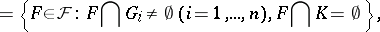 |
for a compact set 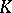 and open sets
and open sets 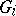 . Let
. Let 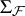 be the Borel
be the Borel 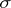 -algebra generated by the hit-or-miss topology. Then
-algebra generated by the hit-or-miss topology. Then 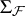 is the smallest
is the smallest 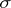 -algebra of subsets of
-algebra of subsets of 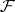 containing the sets
containing the sets
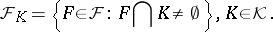 |
Now, a random closed set 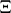 is an
is an 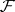 -valued random element. Its distribution is described by the corresponding probability measure
-valued random element. Its distribution is described by the corresponding probability measure 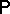 on
on 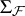 :
:
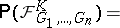 |
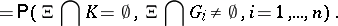 |
This distribution can also be characterized by the functional
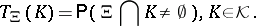 |
The functional 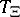 is an alternating Choquet capacity of infinite order. This means that:
is an alternating Choquet capacity of infinite order. This means that:
i) 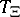 is upper semi-continuous (
is upper semi-continuous (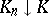 implies
implies 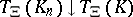 ; cf. also Semi-continuous function);
; cf. also Semi-continuous function);
ii) 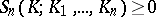 ,
, 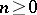 , where
, where
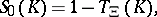 |
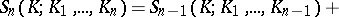 |
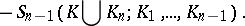 |
The values 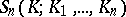 can be interpreted as the probability that
can be interpreted as the probability that 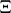 does not intersect
does not intersect 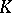 but does intersect
but does intersect 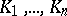 .
.
The Choquet–Kendall–Matheron theorem asserts that given a functional 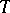 on
on 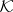 , there exists a distribution
, there exists a distribution 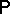 on
on 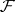 with
with
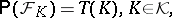 |
if and only if 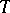 is an alternating Choquet capacity of infinite order with
is an alternating Choquet capacity of infinite order with 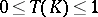 and
and 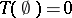 . This distribution is necessarily unique.
. This distribution is necessarily unique.
See [a4] for applications.
References
| [a1] | G. Choquet, "Theory of capacities" Ann. Inst. Fourier , V (1953-1954) pp. 131–295 |
| [a2] | D.G. Kendall, "Foundations of a theory of random sets" E.F. Harding (ed.) D.G. Kendall (ed.) , Stochastic Geometry , Wiley (1974) pp. 322–376 |
| [a3] | G. Matheron, "Random sets and integral geometry" , Wiley (1975) |
| [a4] | D. Stoyan, W.S. Kendall, J. Mecke, "Stochastic geometry and its applications" , Wiley (1995) (Edition: Second) |
Choquet-Kendall-Matheron theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Choquet-Kendall-Matheron_theorem&oldid=22289