Bohr-Mollerup theorem
From Encyclopedia of Mathematics
Revision as of 18:51, 24 March 2012 by Ulf Rehmann (talk | contribs) (moved Bohr–Mollerup theorem to Bohr-Mollerup theorem: ascii title)
The gamma-function on the positive real axis is the unique positive, logarithmically convex function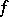 
such that 
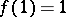and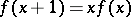 
for all 
.
References
| [a1] | H.P. Boas, "Bohr's power series theorem in several variables" Proc. Amer. Math. Soc. , 125 (1997) pp. 2975–2979 |
| [a2] | C. Caratheodory, "Theory of functions of a complex variable" , 1 , Chelsea (1983) pp. Sects. 274–275 |
How to Cite This Entry:
Bohr-Mollerup theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bohr-Mollerup_theorem&oldid=22155
Bohr-Mollerup theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bohr-Mollerup_theorem&oldid=22155
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article