Banach-Mazur functional

Banach–Mazur operator

A concept of a computable functional (operator), proposed by S. Banach and S. Mazur [1] and concerning the computability of a functional (operator) from a set 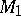into a set 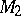as its property to transform any computable sequence of elements of 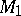into a computable sequence of elements of 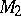(cf. Computable function).

Let 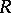be the set of all one-place general recursive functions (cf. General recursive function). A functional 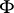defined on 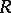and assuming natural numbers as values is called computable according to Banach–Mazur, or a Banach–Mazur functional, if for any two-place general recursive function 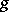there exists a general recursive function 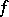such that

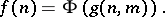(Here 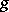is considered to be a function of 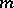for any constant .) All general recursive functionals and everywhere-defined effective functionals (cf. Constructive metric space) are Banach–Mazur functionals. On the other hand, an example of a Banach–Mazur functional which is not identical with any general recursive, and hence neither with any effective, functional is known [2]. An important property of Banach–Mazur functionals is their continuity [1]: The values of such a functional on any general recursive function is defined only by a finite number of values of this function.

The concept of computability just outlined can be extended to functions of a real variable. Let 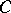be the set of computable sequences of computable real numbers; each sequence 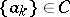is defined by two general recursive functions 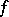and 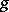such that for all and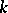

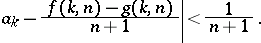A function 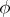of a real variable is said to be computable according to Banach–Mazur (the set of such functions is denoted by 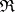) if for any sequence 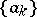from 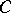the sequence 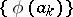also belongs to 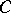. All functions 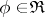are continuous at all computable points [1]. For instance, 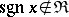. The question as to whether all functions from 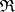are computably continuous is still (1977) open. The set 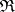is closed with respect to the sequence of operations used in analysis, so that computable analysis can be successfully developed on this basis [1].

References

[1]	S. Mazur, "Computable analysis" , PWN (1963)
[2]	R.M. Friedberg, "4-quantifier completeness: A Banach-Mazur functional not uniformly partial recursive" Bull. Acad. Polon. Sci. Sér. Sci. Math., Astr. Phys. , 6 : 1 (1958) pp. 1–5
[3]	A.A. Markov, "On constructive functions" Trudy Mat. Inst. Steklov. , 52 (1958) pp. 315–348 (In Russian)
[4]	H. Rogers jr., "Theory of recursive functions and effective computability" , McGraw-Hill (1967) pp. 164–165

Comments

For a more recent exposition of recursive analysis, see [a1].

References

[a1]	O. Aberth, "Computable analysis" , McGraw-Hill (1980)