Apéry numbers
The Apéry numbers  ,
,  are defined by the finite sums
are defined by the finite sums
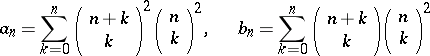 |
for every integer  . They were introduced in 1978 by R. Apéry in his highly remarkable irrationality proofs of
. They were introduced in 1978 by R. Apéry in his highly remarkable irrationality proofs of  and
and  , respectively. In the case of
, respectively. In the case of  , Apéry showed that there exists a sequence of rational numbers
, Apéry showed that there exists a sequence of rational numbers  with denominator dividing
with denominator dividing  such that
such that  for all
for all  . Together with the fact that
. Together with the fact that 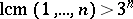 , this implies the irrationality of
, this implies the irrationality of  . For a very lively and amusing account of Apéry's discovery, see [a4]. In 1979 F. Beukers [a1] gave a very short irrationality proof of
. For a very lively and amusing account of Apéry's discovery, see [a4]. In 1979 F. Beukers [a1] gave a very short irrationality proof of  , motivated by the shape of the Apéry numbers. Despite much efforts by many people there is no generalization to an irrationality proof of
, motivated by the shape of the Apéry numbers. Despite much efforts by many people there is no generalization to an irrationality proof of  so far (2001).
so far (2001).
T. Rival [a5] proved the very surprising result that  for infinitely many
for infinitely many  .
.
It did not take long before people noticed a large number of interesting congruence properties of Apéry numbers. For example, 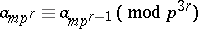 for all positive integers
for all positive integers 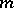 ,
,  and all prime numbers
and all prime numbers  . Another congruence is
. Another congruence is  for all prime numbers
for all prime numbers 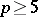 . Here,
. Here,  denotes the coefficient of
denotes the coefficient of 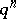 in the
in the  -expansion of a modular cusp form. For more details see [a2], [a3].
-expansion of a modular cusp form. For more details see [a2], [a3].
References
| [a1] | F. Beukers, "A note on the irrationality of 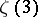 " Bull. London Math. Soc. , 11 (1979) pp. 268–272 " Bull. London Math. Soc. , 11 (1979) pp. 268–272 |
| [a2] | F. Beukers, "Some congruences for the Apéry numbers" J. Number Theory , 21 (1985) pp. 141–155 |
| [a3] | F. Beukers, "Another conguence for the Apéry numbers" J. Number Theory , 25 (1987) pp. 201–210 |
| [a4] | A.J. van der Poorten, "A proof that Euler missed  Apéry's proof of the irrationality of Apéry's proof of the irrationality of 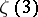 " Math. Intelligencer , 1 (1979) pp. 195–203 " Math. Intelligencer , 1 (1979) pp. 195–203 |
| [a5] | T. Rival, "La fonction zêta de Riemann pren une infinité de valeurs irrationnelles aux entiers impairs" C.R. Acad. Sci. Paris , 331 (2000) pp. 267–270 |
Apéry numbers. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ap%C3%A9ry_numbers&oldid=22025