Uniform subgroup
of a locally compact topological group 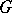
A closed subgroup  such that the quotient space
such that the quotient space  is compact. Closely related to this notion is that of a quasi-uniform subgroup of
is compact. Closely related to this notion is that of a quasi-uniform subgroup of 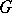 , that is, a closed subgroup
, that is, a closed subgroup 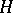 of
of 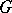 for which there is a
for which there is a 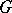 -invariant measure
-invariant measure 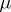 on
on 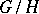 with
with  . For example, the subgroup
. For example, the subgroup  of
of 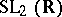 is quasi-uniform, but not uniform. On the other hand, the subgroup
is quasi-uniform, but not uniform. On the other hand, the subgroup 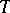 of all upper-triangular matrices in
of all upper-triangular matrices in 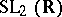 is a uniform subgroup of
is a uniform subgroup of 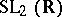 that is not quasi-uniform (there are no
that is not quasi-uniform (there are no 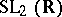 -invariant measures on
-invariant measures on  ). However, every connected quasi-uniform subgroup of a Lie group
). However, every connected quasi-uniform subgroup of a Lie group  is a uniform subgroup (see [1]), and every discrete uniform subgroup of
is a uniform subgroup (see [1]), and every discrete uniform subgroup of 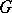 is quasi-uniform [2]. (On the topic of discrete uniform subgroups of Lie groups, see Discrete subgroup.) If
is quasi-uniform [2]. (On the topic of discrete uniform subgroups of Lie groups, see Discrete subgroup.) If 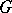 is a connected Lie group and
is a connected Lie group and 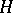 is a uniform subgroup of
is a uniform subgroup of 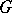 , then the normalizer
, then the normalizer 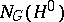 in
in 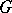 of the connected component of the identity
of the connected component of the identity 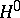 in
in  contains a maximal connected triangular subgroup of
contains a maximal connected triangular subgroup of 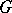 (see [3]). An algebraic subgroup
(see [3]). An algebraic subgroup 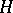 of a connected algebraic complex linear Lie group
of a connected algebraic complex linear Lie group 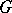 is a uniform subgroup if and only if
is a uniform subgroup if and only if 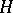 is a parabolic subgroup in
is a parabolic subgroup in  . All connected uniform subgroups of semi-simple Lie groups have been described (see [4]). A non-discrete uniform subgroup
. All connected uniform subgroups of semi-simple Lie groups have been described (see [4]). A non-discrete uniform subgroup 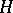 of a connected semi-simple Lie group
of a connected semi-simple Lie group 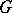 has the property of strong rigidity (see [5]), which is that in
has the property of strong rigidity (see [5]), which is that in 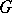 there are a finite number of subgroups
there are a finite number of subgroups 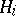 ,
, 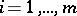 , such that any subgroup
, such that any subgroup 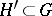 isomorphic to
isomorphic to 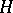 is conjugate to one of the subgroups
is conjugate to one of the subgroups 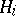 . Important examples of uniform and quasi-uniform subgroups are constructed as follows. Let
. Important examples of uniform and quasi-uniform subgroups are constructed as follows. Let 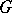 be a linear algebraic group defined over the field of rational numbers
be a linear algebraic group defined over the field of rational numbers 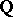 , let
, let 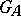 be the adèle group and let
be the adèle group and let  be the subgroup of principal adèles. Then
be the subgroup of principal adèles. Then 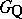 is a discrete subgroup in
is a discrete subgroup in 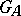 ; moreover,
; moreover, 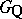 is a uniform subgroup of
is a uniform subgroup of 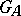 if and only if: 1)
if and only if: 1) 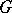 has no non-trivial rational characters defined over
has no non-trivial rational characters defined over 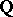 ; and 2) all unipotent elements of
; and 2) all unipotent elements of  belong to its radical (see [6], [7]). In particular, if
belong to its radical (see [6], [7]). In particular, if 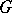 is a unipotent algebraic group defined over
is a unipotent algebraic group defined over 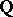 , then
, then 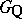 is a uniform subgroup of
is a uniform subgroup of 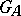 . Condition 1) is necessary and sufficient for the quasi-uniformity of
. Condition 1) is necessary and sufficient for the quasi-uniformity of 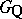 and
and 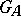 .
.
References
| [1] | G.D. Mostow, "Homogeneous spaces with finite invariant measure" Ann. of Math. , 75 : 1 (1962) pp. 17–37 MR0145007 Zbl 0115.25702 |
| [2] | M.S. Raghunathan, "Discrete subgroups of Lie groups" , Springer (1972) MR0507234 MR0507236 Zbl 0254.22005 |
| [3] | A.L. Onishchik, "Lie groups transitive on compact manifolds" Transl. Amer. Math. Soc. (2) , 73 (1968) pp. 59–72 Mat. Sb. , 71 : 4 (1966) pp. 483–494 Zbl 0198.29001 |
| [4] | A.L. Onishchik, "On Lie groups transitive on compact manifolds II" Math. USSR Sb. , 3 : 3 (1967) pp. 373–388 Mat. Sb. , 74 : 3 (1967) pp. 398–416 Zbl 0198.28903 |
| [5] | M. Goto, H.C. Wang, "Non-discrete uniform subgroups of semisimple Lie groups" Math. Ann. , 198 : 4 (1972) pp. 259–286 MR0354934 Zbl 0228.22014 |
| [6] | A. Borel, "Some properties of adele groups attached to algebraic groups" Bull. Amer. Math. Soc. , 67 : 6 (1961) pp. 583–585 MR0141671 Zbl 0119.37002 |
| [7] | G.D. Mostow, T. Tamagawa, "On the compactness of arithmetically defined homogeneous spaces" Ann. of Math. , 76 : 3 (1962) pp. 446–463 MR0141672 Zbl 0196.53201 |
Uniform subgroup. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Uniform_subgroup&oldid=21957