Adjoint representation of a Lie group
or algebraic group 
The linear representation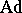 
of 
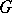in the tangent space 
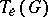(or in the Lie algebra 
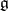of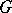 
) mapping each 
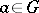to the differential 
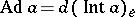of the inner automorphism 
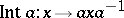. If 
is a linear group in a space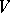 
, then
 |
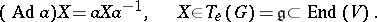The kernel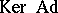 
contains the centre of 
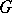, and if 
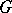is connected and if the ground field has characteristic zero, coincides with this centre. The differential of the adjoint representation of 
at 
coincides with the adjoint representation 
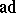of 
.
The adjoint representation of a Lie algebra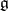 
is the linear representation 
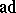of the algebra 
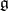into the module 
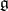acting by the formula
 |
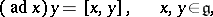where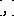 
is the bracket operation in the algebra 
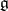. The kernel 
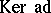is the centre of the Lie algebra 
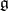. The operators 
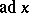are derivations of 
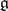and are called inner derivations. The image 
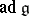is called the adjoint linear Lie algebra and is an ideal in the Lie algebra 
of all derivations of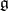 
, moreover 
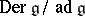is the one-dimensional cohomology space 
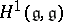of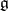 
, defined by the adjoint representation. In particular, 
if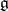 
is a semi-simple Lie algebra over a field of characteristic zero.
References
| [1] | N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979)) MR0148716 MR0143793 Zbl 0121.27504 Zbl 0109.26201 |
| [2] | L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) MR0201557 Zbl 0022.17104 |
| [3] | J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) MR0218496 Zbl 0132.27803 |
| [4] | J.E. Humphreys, "Linear algebraic groups" , Springer (1975) MR0396773 Zbl 0325.20039 |
Comments
References
| [a1] | N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) pp. Chapt. 2; 3 (Translated from French) MR0682756 Zbl 0319.17002 |
Adjoint representation of a Lie group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Adjoint_representation_of_a_Lie_group&oldid=21801