Linear function
A function of the form  . The main property of a linear function is: The increment of the function is proportional to the increment of the argument. Graphically a linear function is represented by a straight line.
. The main property of a linear function is: The increment of the function is proportional to the increment of the argument. Graphically a linear function is represented by a straight line.
A linear function in  variables
variables  is a function of the form
is a function of the form
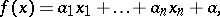 |
where  and
and  are certain fixed numbers. The domain of definition of a linear function is the whole
are certain fixed numbers. The domain of definition of a linear function is the whole  -dimensional space of the variables
-dimensional space of the variables  , real or complex. If
, real or complex. If  , the linear function is called a homogeneous, or linear, form.
, the linear function is called a homogeneous, or linear, form.
If all variables  and coefficients
and coefficients 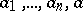 are real (complex) numbers, then the graph of the linear function in the
are real (complex) numbers, then the graph of the linear function in the 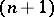 -dimensional (complex) space of the variables
-dimensional (complex) space of the variables 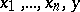 is the (complex)
is the (complex)  -dimensional hyperplane
-dimensional hyperplane  , in particular, for
, in particular, for  it is a straight line in the plane (respectively, a complex plane in two-dimensional complex space).
it is a straight line in the plane (respectively, a complex plane in two-dimensional complex space).
The term "linear function" , or, more precisely, homogeneous linear function, is often used for a linear mapping of a vector space 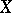 over a field
over a field 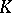 into this field, that is, for a mapping
into this field, that is, for a mapping 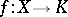 such that for any elements
such that for any elements  and any
and any  ,
,
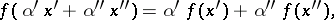 |
and in this case instead of the term "linear function" one also uses the terms linear functional and linear form.
Linear function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_function&oldid=19728