Vandermonde determinant
A determinant of order  of the type
of the type
 | (*) |
where  are elements of a commutative ring. For any
are elements of a commutative ring. For any  ,
,
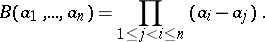 |
If the ring has no zero divisors, the fundamental property of a Vandermonde determinant holds: 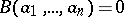 if and only if not all the elements
if and only if not all the elements  are different from each other. The determinant was first studied by A.T. Vandermonde for the case
are different from each other. The determinant was first studied by A.T. Vandermonde for the case 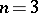 , and then in 1815 by A.L. Cauchy .
, and then in 1815 by A.L. Cauchy .
References
| [1a] | A.T. Vandermonde, Histoire Acad. R. Sci. Paris (1771 (1774)) pp. 365–416 |
| [1b] | A.T. Vandermonde, Histoire Acad. R. Sci. Paris (1772 (1776)) pp. 516–532 |
| [2a] | A.A. Cauchy, "Mémoire sur les fonctions qui ne peuvent obtenir que deux values" J. École Polytechnique , 17 : 10 (1815) pp. 29- |
| [2b] | A.L. Cauchy, "Mémoire sur les fonctions qui ne peuvent obtenir que deux values" , Oeuvres Sér. 2 , 1 , Gauthier-Villars (1905) pp. 91–169 |
Comments
The matrix
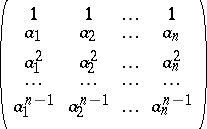 |
participating in (*) is called a Vandermonde matrix.
The Vandermonde matrix plays a role in approximation theory. E.g., using it one can prove that there is a unique polynomial of degree  taking prescribed values at
taking prescribed values at 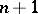 distinct points, cf. [a1], p. 58. See [a1], p. 64, Problem 13, for an algorithm to compute the inverse of a Vandermonde matrix.
distinct points, cf. [a1], p. 58. See [a1], p. 64, Problem 13, for an algorithm to compute the inverse of a Vandermonde matrix.
References
| [a1] | E.W. Cheney, "Introduction to approximation theory" , Chelsea, reprint (1982) |
Vandermonde determinant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vandermonde_determinant&oldid=19300