Maximal correlation coefficient
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
A measure of dependence of two random variables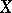 
and 
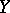, defined as the least upper bound of the values of the correlation coefficients between the real random variables 
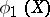and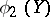 
, which are functions of 
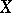and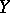 
such that 
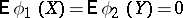and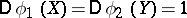 
:
 |
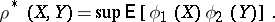If this least upper bound is attained at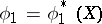 
and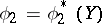 
, then the maximal correlation coefficient between 
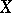and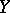 
is equal to the correlation coefficient of 
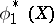and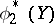 
. The maximal correlation coefficient has the property: 
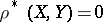is necessary and sufficient for the independence of 
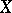and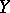 
. If there is a linear correlation between the variables, then the maximal correlation coefficient coincides with the usual correlation coefficient.
References
| [1] | O.V. Sarmanov, "The maximum correlation coefficient (symmetric case)" Dokl. Akad. Nauk SSSR , 120 : 4 (1958) pp. 715–718 (In Russian) |
| [2] | O.V. Sarmanov, Dokl. Akad. Nauk SSSR , 53 : 9 (1946) pp. 781–784 |
| [3] | Yu.V. [Yu.V. Prokhorov] Prohorov, Yu.A. Rozanov, "Probability theory, basic concepts. Limit theorems, random processes" , Springer (1969) (Translated from Russian) |
Comments
See also Canonical correlation.
References
| [a1] | H. Gebelein, "Das statistische Problem der Korrelation als Variations- und Eigenwertproblem und sein Zusammenhang mit der Ausgleichungrechnung" Z. Angew. Math. Mech. , 21 (1941) pp. 364–379 |
| [a2] | R. Koyak, "On measuring internal dependence in a set of random variables" Ann. Statist. , 15 (1987) pp. 1215–1229 |
How to Cite This Entry:
Maximal correlation coefficient. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximal_correlation_coefficient&oldid=19195
Maximal correlation coefficient. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximal_correlation_coefficient&oldid=19195
This article was adapted from an original article by I.O. Sarmanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article