Minimax property

of eigen values

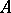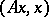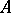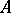A special type of relationship connecting the eigen values of a completely-continuous self-adjoint operator (cf. also Completely-continuous operator) with the maximum and minimum values of the associated quadratic form . Let be a completely-continuous self-adjoint operator on a Hilbert space . The spectrum of consists of a finite or countable set of real eigen values 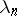having unique limit point zero. The root subspaces corresponding to the non-zero eigen values consist of eigen vectors and are finite dimensional; the eigen subspaces associated with distinct eigen values are mutually orthogonal; 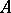has a complete system of eigen vectors. The spectral decomposition of 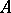(cf. Spectral decomposition of a linear operator) has the form: 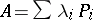, where are the distinct eigen values, 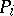are the projection operators onto the corresponding eigen spaces, and the series converges in the operator norm. The norm of 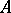coincides with the maximum modulus of the eigen values and with 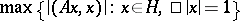; the maximum is attained at the corresponding eigen vector.

Let 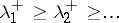be the positive eigen values of 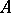, where each eigen value is repeated as often as its multiplicity. Then

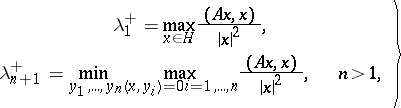(1)

where 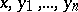are arbitrary non-zero vectors in 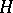. Similar relations hold for the negative eigen values :

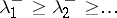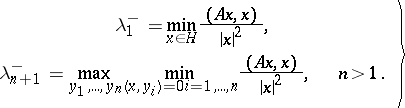(2)

Relations (1) and (2) are applied for finding the eigen values of integral operators with a symmetric kernel. If 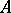and 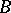are completely-continuous self-adjoint operators, 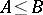(that is, 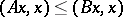), and 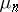the sequences of their positive eigen values, listed in decreasing order, where each value is repeated as often as its multiplicity, then .

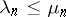References

[1]	N. Dunford, J.T. Schwartz, "Linear operators. Spectral theory" , 2 , Wiley (1988)