Subvariety, involutive

(in symplectic geometry)

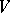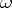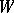Let be a vector space of dimension and a non-degenerate alternating -form on it. Given a subspace of 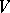, one defines (as usual)

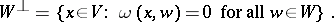One says that 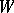is an isotropic subspace if 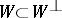, that it is an involutive subspace (or co-isotropic subspace) if 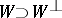, and that it is a Lagrangian subspace if 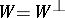. Note that for 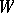to be involutive it is necessary that .

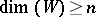Now, let 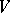be a subvariety (possibly with singularities; or, more generally, an analytic subset) of a symplectic manifold 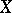. Let 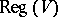be the set of points of 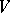which have a neighbourhood in 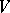that is free of singular points. Then 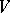is an involutive subvariety of 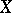if for all 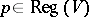the subspace 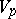of 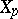is involutive. The notions of an isotropic subvariety and a Lagrangian subvariety are defined analogously. If 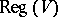is dense in 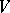, then 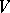is involutive if and only if for every two 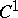-functions 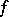, 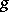on 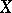which vanish on 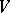the Poisson bracket 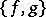(defined by the symplectic -form on 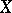) also vanishes on .

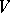References

[a1]	P. Libermann, C.-M. Marle, "Symplectic geometry and analytical mechanics" , Reidel (1987) (Translated from French)