Macdonald function
modified cylinder function, Bessel function of imaginary argument
A function
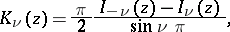 |
where  is an arbitrary non-integral real number and
is an arbitrary non-integral real number and
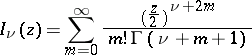 |
is a cylinder function with pure imaginary argument (cf. Cylinder functions). They have been discussed by H.M. Macdonald [1]. If  is an integer, then
is an integer, then
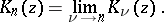 |
The Macdonald function  is the solution of the differential equation
is the solution of the differential equation
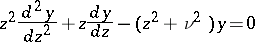 | (*) |
that tends exponentially to zero as  and takes positive values. The functions
and takes positive values. The functions  and
and 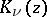 form a fundamental system of solutions of (*).
form a fundamental system of solutions of (*).
For 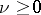 ,
, 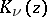 has roots only when
has roots only when 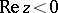 . If
. If 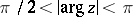 , then the number of roots in these two sectors is equal to the even number nearest to
, then the number of roots in these two sectors is equal to the even number nearest to 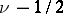 , provided that
, provided that  is not an integer; in the latter case the number of roots is equal to
is not an integer; in the latter case the number of roots is equal to  . For
. For 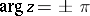 there are no roots if
there are no roots if 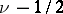 is not an integer.
is not an integer.
Series and asymptotic representations are:
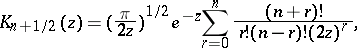 |
where  is a non-negative integer;
is a non-negative integer;
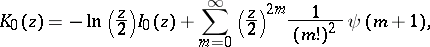 |
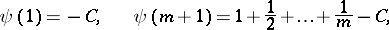 |
where 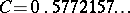 is the Euler constant;
is the Euler constant;
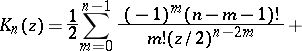 |
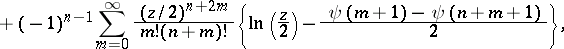 |
where 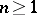 is an integer;
is an integer;
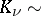 |
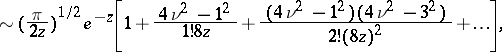 |
for large  and
and 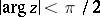 .
.
Recurrence formulas:
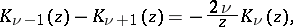 |
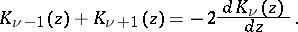 |
References
| [1] | H.M. Macdonald, "Zeroes of the Bessel functions" Proc. London Math. Soc. , 30 (1899) pp. 165–179 |
| [2] | G.N. Watson, "A treatise on the theory of Bessel functions" , 1–2 , Cambridge Univ. Press (1952) |
Macdonald function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Macdonald_function&oldid=19172