Two-dimensional knot

A class of isotopic imbeddings of the two-dimensional sphere in the four-dimensional one . The condition of local planarity is usually imposed. The method of study consists in considering sections of by a bundle of three-dimensional parallel planes. The fundamental problem is whether or not the knot will be trivial if its group 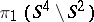is isomorphic to 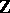. It is known that in such a case the complement 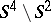has the homotopy type of .

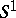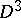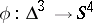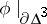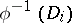A -ribbon in is the image of an immersion , where is the three-dimensional disc, such that: 1) is an imbedding; 2) the self-intersection of consists of a finite number of pairwise non-intersecting two-dimensional discs ; and 3) the pre-image of each disc is a union of two discs and 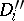such that

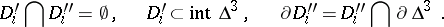The image of the boundary is a two-dimensional knot in . The knots thus obtained are said to be ribbon knots. This is one of the most thoroughly studied class of two-dimensional knots. Any two-dimensional ribbon knot is the boundary of some three-dimensional submanifold of the sphere which is homeomorphic either to the disc or to the connected sum of some number of 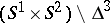. A two-dimensional ribbon knot is trivial if and only if the fundamental group of its complement is isomorphic to 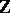. A group 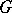is the group of some two-dimensional ribbon knot in if and only if it has a Wirtinger presentation (i.e. a presentation , where each relation has the form ) in which the number of relations is one smaller than the number of generators and .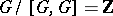

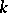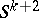The class of groups of all two-dimensional knots has not yet been fully described. It is known that this class is wider than that of the one-dimensional knots in but smaller than the class of groups of -dimensional knots in , . The latter class has been fully characterized (cf. Multi-dimensional knot). The following properties are displayed by two-dimensional knot groups (but not, in general, by the groups of three-dimensional knots in ):

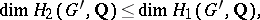where 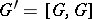is the commutator subgroup; on the finite group 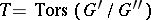there exists a non-degenerate symmetric form 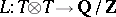such that for any , one has 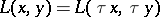, where is the automorphism induced in by conjugation with the element .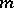

The calculation of 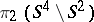has been done only for special types of two-dimensional knots, e.g. those obtained by Artin's construction, ribbon knots and fibred knots.