Circle problem

The problem of obtaining the best asymptotic estimate for the number of lattice points in the disc 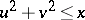. Let 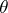be the greatest lower bound of the numbers 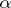in the equality

(*)

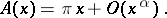C.F. Gauss proved that 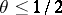(see [1]). W. Sierpiński, using G.F. Voronoi's method [3], proved that (see [2]). In [4] it was shown that . The most recent (1987) estimate is 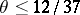. There is a conjecture that the remainder term in formula (*) is

There is a mean-value theorem for the circle problem:

where 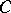is some absolute constant and 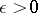is arbitrary.

In terms of its content and the methods used to attack it, the circle problem is largely analogous to Dirichlet's divisor problem (see Divisor problems). A generalization of the circle problem is the sphere problem — the problem of an estimate for , the number of lattice points in the ball 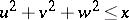. A basis for such an estimate is the formula

where

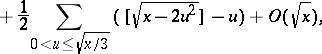which is established by partitioning the ball into 24 sections by the six planes

where each section contains the same number of lattice points, provided one counts points on the sectioning planes with coefficients . The principal term of growth of 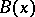is equal to the volume of the ball

hence the problem reduces to estimating , which is the sum of the fractional parts of the functions in square brackets in the formula for 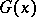. The most profound estimates for have been obtained using I.M. Vinogradov's method of trigonometric sums [5], [6]:

There is a conjecture that

A generalization of the circle and sphere problems is the problem of estimating , the number of lattice points in -dimensional ellipsoids

where 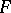is a positive-definite quadratic form [7].

References

[1]	C.F. Gauss, , Werke , 2 , Göttingen (1863) pp. 269–291
[2]	W. Sierpiński, Prace Mat. Fiz. , 17 (1906) pp. 77–118
[3]	G.F. Voronoi, , Collected works , 1 , Kiev (1952) pp. 5 (In Russian)
[4]	L.-K. Hua, "The method of trigonometric sums and its applications to number theory" , Selected papers , Springer (1983) pp. 124–135 (Translated from German)
[5]	I.M. Vinogradov, "On the number of integer points in a ball" Izv. Akad. Nauk SSSR Ser. Mat. , 27 : 5 (1963) pp. 957–968 (In Russian)
[6]	I.M. Vinogradov, "Basic variants of the method of trigonometric sums" , Moscow (1976) (In Russian)
[7]	B. Novák, "Lattice points in more-dimensional ellipsoids" Trudy Mat. Inst. Akad. Nauk SSSR , 132 (1973) pp. 145–150 (In Russian)

Comments

The most recent estimate referred to above, 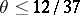, was obtained in 1963 by J. Chen [a1]. The circle problem is also known as the Gauss circle problem.

References

[a1]	J. Chen, "The lattice-points in a circle" Sci. Sinica , 12 (1963) pp. 633–649
[a2]	A.Z. Walfisz, "Gitterpunkte in mehrdimensionalen Kugeln" , PWN (1957)