Menelaus theorem
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
A theorem on the relations between the lengths of the segments on the sides of a triangle determined by an intersecting straight line. It asserts that if the given line intersects the sides of a triangle 
(or their extensions) at the points 
, 
and 
, then
 |
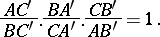Menelaus' theorem is a particular case of the Carnot theorem; it can be generalized to the case of a polygon. Thus, suppose that a straight line 
intersects the edges 
of a polygon 
at the respective points 
. Then the following relation is valid:
 |
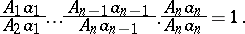The theorem was proved by Menelaus (1st century) and apparently it was known to Euclid (3rd century B.C.).
Figure: m063400a
Comments
References
| [a1] | B.L. van der Waerden, "Science awakening" , 1 , Noordhoff & Oxford Univ. Press (1961) pp. 275 (Translated from Dutch) |
How to Cite This Entry:
Menelaus theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Menelaus_theorem&oldid=19060
Menelaus theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Menelaus_theorem&oldid=19060
This article was adapted from an original article by P.S. Modenov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article