Wiener measure(2)

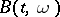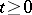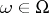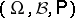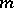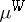The probability distribution of a Brownian motion , , , where is a probability space. The Wiener measure is denoted by or . Brownian motion 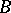is a Gaussian process such that

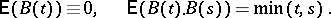Given a Brownian motion 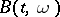, one can form a new Brownian motion 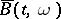satisfying:

i) 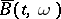is continuous in for almost all .

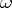ii) 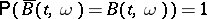for every .

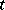Such a process 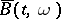is called a continuous version of .

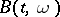The Kolmogorov–Prokhorov theorem tells that the probability distribution 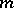of the Brownian motion 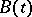can be introduced in the space 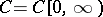of all continuous functions on .

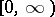Let 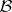be the topological Borel field (cf. also Borel field of sets) of subsets of 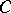. The measure space 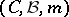thus obtained is the Wiener measure space.

The integral of a 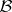-measurable functional on 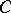with respect to 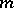is defined in the usual manner. (See also Stochastic integral.)

An elementary and important example of a 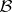-measurable functional of 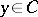is a stochastic bilinear form, given by 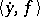, where 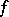is an -function. It is usually denoted by 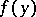. It is, in fact, defined by 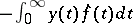for smooth functions 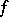. For a general 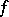, 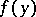can be approximated by stochastic bilinear forms defined by smooth functions 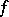. An integral of this type is called a Wiener integral. Under certain restrictions, such as non-anticipation, the integral can be extended to the case where the integrand is a functional of 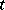and 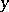. And an even more general case has been proposed.

The class of general (non-linear) functionals of 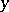is introduced as follows. Let 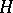be the Hilbert space of all complex-valued, square--integrable functionals on 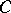. Then, 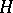admits a direct sum decomposition (Fock space)

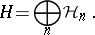The subspace 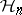is spanned by the Fourier–Hermite polynomials of degree , which are of the form

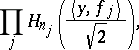where and 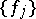is a complete orthonormal system in the Hilbert space 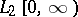. The space 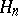can be interpreted as the space of multiple Wiener integrals of degree , due to K. Itô.

References

[a1]	R. Cameron, W.T. Martin, "The orthogonal development of non-linear functionals in series of Fourier–Hermite functionals" Ann. of Math. (2) , 48 pp. 385–392
[a2]	T. Hida, "Brownian motion" , Applications of Mathematics , 11 , Springer (1980)