Iterated kernel
From Encyclopedia of Mathematics
A function 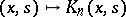 that is formed from the given kernel
that is formed from the given kernel  of an integral operator (cf. Kernel of an integral operator)
of an integral operator (cf. Kernel of an integral operator)
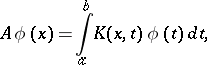 |
by the recurrence relations
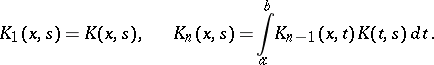 |
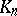 is called the
is called the  -th iterate, or
-th iterate, or  -th iterated kernel, of
-th iterated kernel, of 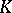 . An iterated kernel is sometimes called a repeated kernel. If
. An iterated kernel is sometimes called a repeated kernel. If  is a continuous or square-integrable kernel, then all its iterates are continuous, respectively, square integrable. If
is a continuous or square-integrable kernel, then all its iterates are continuous, respectively, square integrable. If 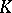 is a symmetric kernel, so are all its iterates. The kernel
is a symmetric kernel, so are all its iterates. The kernel 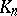 is the kernel of the operator
is the kernel of the operator 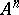 . The equality
. The equality
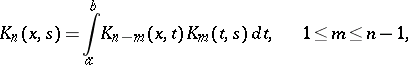 |
holds.
References
| [1] | V.I. Smirnov, "A course of higher mathematics" , 4 , Addison-Wesley (1964) pp. Chapt. 1 (Translated from Russian) |
| [2] | S.G. Mikhlin, "Linear integral equations" , Hindushtan Publ. Comp. , Delhi (1960) (Translated from Russian) |
Comments
References
| [a1] | I.C. Gohberg, S. Goldberg, "Basic operator theory" , Birkhäuser (1981) |
| [a2] | P.P. Zabreiko (ed.) A.I. Koshelev (ed.) M.A. Krasnoselskii (ed.) S.G. Mikhlin (ed.) L.S. Rakovshchik (ed.) V.Ya. Stet'senko (ed.) T.O. Shaposhnikova (ed.) R.S. Anderssen (ed.) , Integral equations - a reference text , Noordhoff (1975) (Translated from Russian) |
How to Cite This Entry:
Iterated kernel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Iterated_kernel&oldid=18997
Iterated kernel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Iterated_kernel&oldid=18997
This article was adapted from an original article by B.V. Khvedelidze (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article