Eberlein compactum

An Eberlein compactum is a compactum 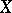that is homeomorphic to a subset of a Banach space with the weak topology [a3].

W.A. Eberlein showed [a1] that such spaces are sequentially compact and Fréchet–Urysohn spaces (cf. Sequentially-compact space; Fréchet space).

One has the following structure theorem for Eberlein compacta: For a compactum 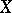the following are equivalent: i) 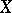is an Eberlein compactum; ii) 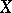is homeomorphic to a subset of 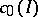in the weak topology (or, equivalently, the pointwise topology), for some set 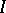; and iii) 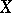has a family 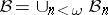of open 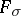-sets such that each family 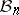is point-finite and for every 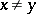there is a 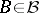containing exactly one of and .

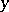Here 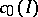is the Banach space .

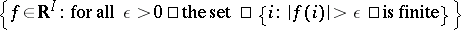The class of Eberlein compact spaces is closed under taking closed subspaces, continuous images and countable products. A recent characterization of Eberlein compact spaces reads as follows [a2]: 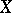is an Eberlein compact space if and only if every subspace of 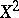is 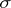-metacompact, where 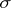-metacompactness means that every open covering has an open refinement which is a union of countably many point-finite families.

A good survey can be found in [a4].

References

[a1]	W.A. Eberlein, "Weak compactness in Banach spaces" Proc. Nat. Acad. Sci. USA , 33 (1947) pp. 51–53
[a2]	G. Gruenhage, "Games, covering properties and Eberlein compacts" Topology Appl. , 23 (1986) pp. 291–297
[a3]	J. Lindenstrauss, "Weakly compact sets - their topological properties and the Banach spaces they generate" , Symp. infinite-dimensional topology , Ann. Math. Studies , 69 , Princeton Univ. Press (1972) pp. 235–276
[a4]	S. Negrepontis, "Banach spaces and topology" K. Kunen (ed.) J.E. Vaughan (ed.) , Handbook of set-theoretic topology , North-Holland (1984) pp. 1054–1142