Lindelöf hypothesis
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
Lindelöf conjecture, on the behaviour of the Riemann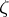 
-function
For any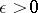 
,
 |
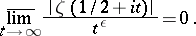It was stated by E. Lindelöf [1]. The Lindelöf conjecture is equivalent to the assertion that for a fixed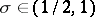 
the number of zeros of 
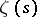that lie in the domain 
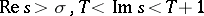is 
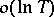. The Lindelöf conjecture is therefore a consequence of the Riemann conjecture on the zeros of 
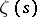(cf. Riemann hypotheses). It is known (1982) that
 |
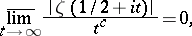where 
is a constant such that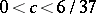 
.
There is a generalization of the Lindelöf conjecture to Dirichlet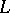 
-functions: For any 
,
 |
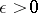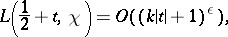where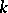 
is the modulus of the character 
.
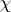References
| [1] | E. Lindelöf, "Le calcul des résidus et ses applications à la théorie des fonctions" , Gauthier-Villars (1905) |
| [2] | E.C. Titchmarsh, "The theory of the Riemann zeta-function" , Oxford Univ. Press (1951) pp. Chapt. 13 |
Comments
References
| [a1] | A. Ivic, "The Riemann zeta-function" , Wiley (1985) |
How to Cite This Entry:
Lindelöf hypothesis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lindel%C3%B6f_hypothesis&oldid=18908
Lindelöf hypothesis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lindel%C3%B6f_hypothesis&oldid=18908
This article was adapted from an original article by S.M. Voronin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article