Degenerate kernels, method of
A method to construct an approximating equation for approximate (and numerical) solutions of certain kinds of linear and non-linear integral equations. The main type of integral equations suitable for solving by this method are linear one-dimensional integral Fredholm equations of the second kind. The method as applied to such equations consists of an approximation which replaces the kernel 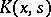 of the integral equation
of the integral equation
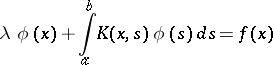 | (1) |
by a degenerate kernel of the type
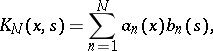 |
followed by the solution of the Fredholm degenerate integral equation
 | (2) |
Solving (2) is reduced to solving a system of linear algebraic equations. The degenerate kernel 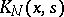 may be found from the kernel
may be found from the kernel 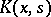 in several ways, e.g. by expanding the kernel into a Taylor series or a Fourier series (for other methods see Bateman method; Strip method (integral equations)).
in several ways, e.g. by expanding the kernel into a Taylor series or a Fourier series (for other methods see Bateman method; Strip method (integral equations)).
The method of degenerate kernels may be applied to systems of integral equations of the type (1), to multi-dimensional equations with relatively simple domains of integration and to certain non-linear equations of Hammerstein type (cf. Hammerstein equation).
References
| [1] | L.V. Kantorovich, V.I. Krylov, "Approximate methods of higher analysis" , Noordhoff (1958) (Translated from Russian) |
Comments
References
| [a1] | C.T.H. Baker, "The numerical treatment of integral equations" , Clarendon Press (1977) pp. Chapt. 4 |
| [a2] | K.E. Atkinson, "A survey of numerical methods for the solution of Fredholm integral equations of the second kind" , SIAM (1976) |
| [a3] | I.C. Gohberg, S. Goldberg, "Basic operator theory" , Birkhäuser (1981) |
| [a4] | B.L. Moiseiwitsch, "Integral equations" , Longman (1977) |
Degenerate kernels, method of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Degenerate_kernels,_method_of&oldid=18830